Đề bài
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\).
Chu vi tam giác bằng tổng ba cạnh.
Diện tích tam giác bằng một nửa chiều cao nhân cạnh đáy tương ứng.
Lời giải chi tiết
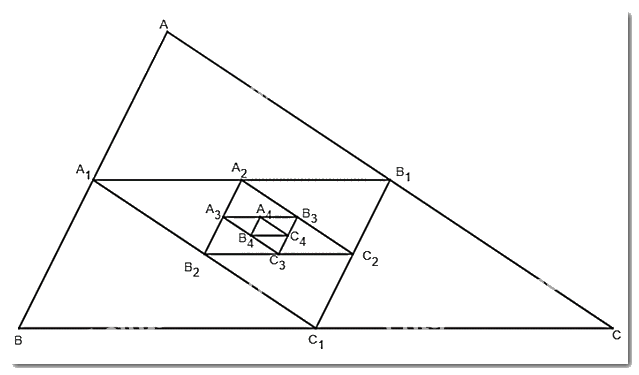
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
