Lý Thuyết Phép Tính Lôgarit - Toán 11 Cánh Diều

Lý thuyết Phép tính lôgarit - Toán 11 Cánh diều

Tổng quan nội dung

Lý thuyết Phép tính Lôgarit - Toán 11 Cánh Diều

Chào mừng bạn đến với bài học về Lý thuyết Phép tính Lôgarit trong chương trình Toán 11 Cánh Diều.

Đây là một trong những chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn.

Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, các dạng bài tập thường gặp và phương pháp giải chúng.

1. Khái niệm lôgarit a) Định nghĩa

1. Khái niệm lôgarit

a) Định nghĩa

Với a > 0, a \( \ne \) 1 và b > 0, ta có: \(c = {\log _a}b \Leftrightarrow {a^c} = b\). Ngoài ra:

- Lôgarit thập phân của b là lôgarit cơ số 10 của số thực dương b:

\(c = \log b \Leftrightarrow {10^c} = b\)

- Lôgarit tự nhiên của b là lôgarit cơ số e của số thực dương b:

\(c = \ln b \Leftrightarrow {e^c} = b\).

b) Tính chất

Với a > 0, a \( \ne \) 1 và b > 0, ta có:

\({\log _a}1 = 0\); \({\log _a}a = 1\); \({\log _a}{a^c} = c\); \({a^{{{\log }_a}b}} = b\).

2. Một số tính chất của phép tính lôgarit

Trong mục này, ta xét a > 0, a \( \ne \) 1 và b > 0.

a) Lôgarit của một tích, một thương

Với m > 0, n > 0, ta có:

\({\log _a}\left( {mn} \right) = {\log _a}m + {\log _a}n\);
\({\log _a}\left( {\frac{m}{n}} \right) = {\log _a}m - {\log _a}n\).

Nhận xét: \({\log _a}\left( {\frac{1}{b}} \right) = - {\log _a}b\).

b) Lôgarit của một lũy thừa

Với mọi số thực \(\alpha \), ta có: \({\log _a}{b^\alpha } = \alpha {\log _a}b\).

Nhận xét: Với mọi số nguyên dương \(n \ge 2\), ta có: \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\).

c) Đổi cơ số của lôgarit

Với a, b là hai số thực dương khác 1 và c là số thực dương, ta có: \({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\).

Nhận xét: Với a, b là hai số thực dương khác 1, c > 0 và \(\alpha \ne 0\), ta có những công thức sau:

\({\log _a}b.{\log _b}c = {\log _a}c\);
\({\log _a}b = \frac{1}{{{{\log }_b}a}}\);
\({\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b\).

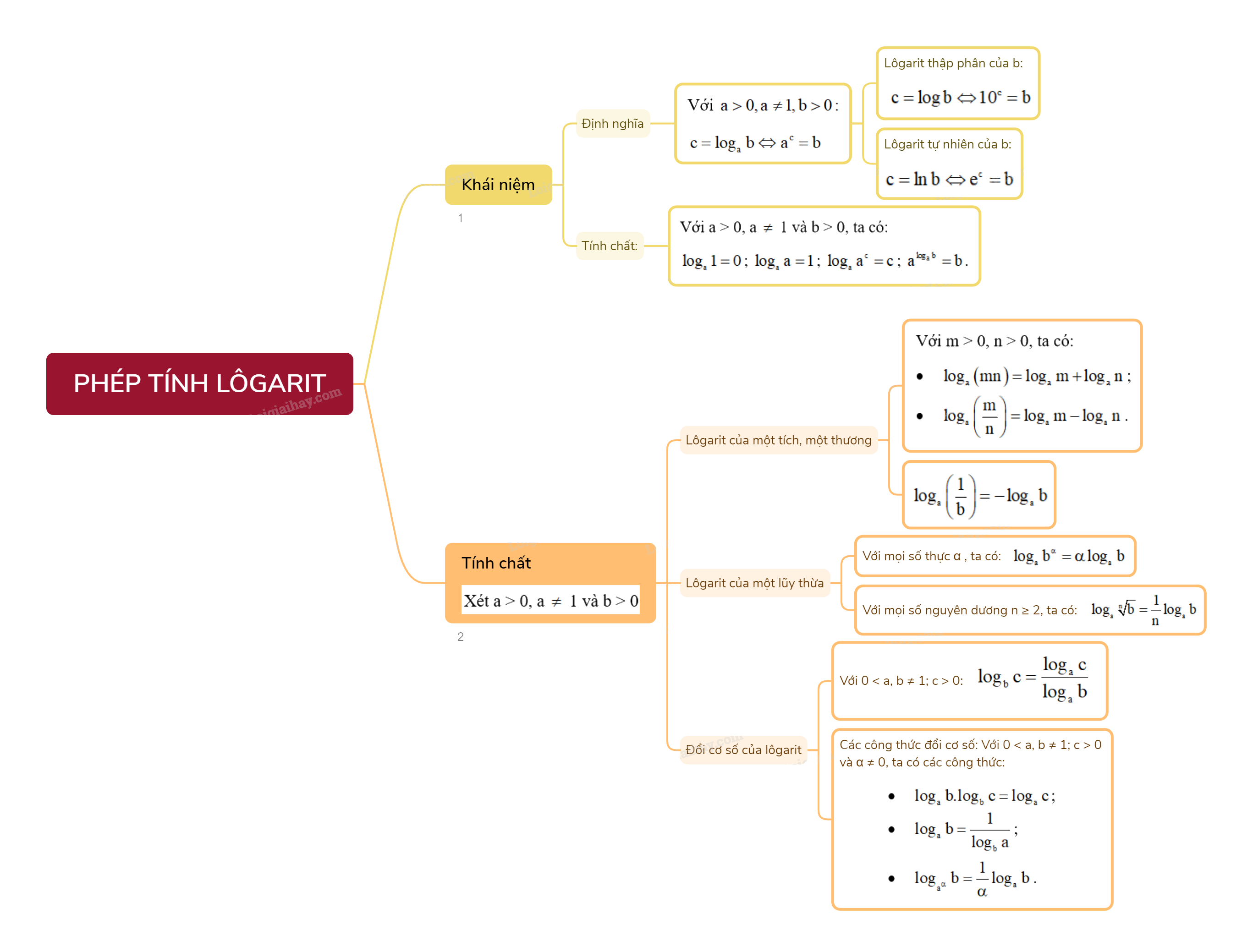
Lý thuyết Phép tính lôgarit - Toán 11 Cánh diều 1

Lý Thuyết Phép Tính Lôgarit - Toán 11 Cánh Diều: Tổng Quan Chi Tiết

Phép tính lôgarit là một trong những khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 11. Nó đóng vai trò then chốt trong việc giải quyết nhiều bài toán liên quan đến hàm số mũ, phương trình và bất phương trình. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết phép tính lôgarit theo chương trình Toán 11 Cánh Diều.

1. Định Nghĩa Lôgarit

Lôgarit của một số dương b (với b ≠ 1) với cơ số a dương (a ≠ 1) là số x sao cho a^x = b. Ký hiệu: log_ab = x.

a: Cơ số của lôgarit (a > 0 và a ≠ 1)
b: Số bị lôgarit (b > 0)
x: Lôgarit cơ số a của b

2. Tính Chất Cơ Bản của Lôgarit

Dưới đây là một số tính chất quan trọng của lôgarit mà bạn cần nắm vững:

log_a1 = 0 (với a > 0 và a ≠ 1)
log_aa = 1 (với a > 0 và a ≠ 1)
log_a(xy) = log_ax + log_ay (với x > 0, y > 0, a > 0 và a ≠ 1)
log_a(x/y) = log_ax - log_ay (với x > 0, y > 0, a > 0 và a ≠ 1)
log_axⁿ = n.log_ax (với x > 0, a > 0 và a ≠ 1)
log_ab = 1/log_ba (với a > 0, a ≠ 1, b > 0 và b ≠ 1)
log_abⁿ = n.log_ab

3. Đổi Cơ Số Lôgarit

Khi cần tính lôgarit với một cơ số khác, ta có thể sử dụng công thức đổi cơ số:

log_ab = log_cb / log_ca (với a > 0, a ≠ 1, b > 0, c > 0 và c ≠ 1)

4. Các Dạng Bài Tập Thường Gặp

Trong chương trình Toán 11 Cánh Diều, các bài tập về lôgarit thường xoay quanh các chủ đề sau:

Tính giá trị của biểu thức lôgarit
Rút gọn biểu thức lôgarit
Giải phương trình lôgarit
Giải bất phương trình lôgarit
Ứng dụng lôgarit vào các bài toán thực tế

5. Ví Dụ Minh Họa

Ví dụ 1: Tính log₂8

Giải: log₂8 = log₂2³ = 3

Ví dụ 2: Rút gọn biểu thức log₃9 + log₃27

Giải: log₃9 + log₃27 = log₃3² + log₃3³ = 2 + 3 = 5

6. Lưu Ý Quan Trọng

Khi làm bài tập về lôgarit, bạn cần lưu ý những điều sau:

Kiểm tra điều kiện xác định của lôgarit (số bị lôgarit phải dương, cơ số phải dương và khác 1)
Sử dụng thành thạo các tính chất của lôgarit để rút gọn biểu thức và giải phương trình
Áp dụng công thức đổi cơ số khi cần thiết

7. Bài Tập Luyện Tập

Bài tập	Đáp án
Tính log₅25	2
Rút gọn log₂16 - log₂4	2

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết phép tính lôgarit trong chương trình Toán 11 Cánh Diều. Chúc bạn học tập tốt!