Bài 6 trang 120 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Bài 6 trang 120 SGK Toán 11 tập 1 - Cánh Diều
Bài 6 thuộc chương trình Toán 11 tập 1, sách Cánh Diều, tập trung vào việc ôn tập chương 1: Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, tích vô hướng để giải quyết các bài toán hình học.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, SD. Xác định giao tuyến của mặt phẳng (AMN) với mỗi mặt phẳng sau:
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, SD. Xác định giao tuyến của mặt phẳng (AMN) với mỗi mặt phẳng sau:
a) (SCD);
b) (SBC).
Phương pháp giải - Xem chi tiết
Tìm 2 điểm cùng thuộc 2 mặt phẳng đó. Đường thẳng đi qua 2 điểm đó chính là giao tuyến của 1 mặt phẳng.
Lời giải chi tiết
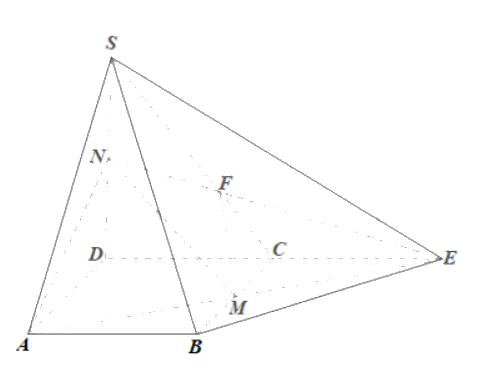
a) Trong mp(ABCD), kéo dài AM cắt DC tại E. Nối SE, BE.
Ta có: E ∈ AM mà AM ⊂ (AMN) nên E ∈ (AMN);
E ∈ DC mà DC ⊂ (SCD) nên E ∈ (SCD).
Do đó E là giao điểm của hai mặt phẳng (AMN) và (SCD).
Lại có: N ∈ SD và SD ⊂ (SCD) nên N ∈ (SCD).
Mà N ∈ (AMN), nên N cũng là giao điểm của hai mặt phẳng (AMN) và (SCD).
Vậy (AMN) ∩ (SCD) = NE.
b) Trong mp(SCD), gọi F là giao điểm của SC và NE.
Ta có: F ∈ NE mà NE ⊂ (AMN) nên F ∈ (AMN);
F ∈ SC mà SC ⊂ (SBC) nên F ∈ (SBC).
Do đó F là giao điểm của (AMN) và (SBC).
Lại có: M ∈ BC và BC ⊂ (SBC) nên M ∈ (SBC).
Mà M ∈ (AMN), nên M cũng là giao điểm của hai mặt phẳng (AMN) và (SBC).
Vậy (AMN) ∩ (SBC) = MF.
Bài 6 trang 120 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn
Bài 6 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong giải quyết các bài toán hình học. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 6 yêu cầu học sinh thực hiện các thao tác sau:
- Cho các điểm A, B, C, D. Tìm tọa độ của các vectơ.
- Tính tích vô hướng của các cặp vectơ.
- Kiểm tra xem hai vectơ có vuông góc hay không.
- Chứng minh một điểm nằm trên đường thẳng.
Lời giải chi tiết
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
- Tọa độ của vectơ: Nếu A(xA; yA) và B(xB; yB) thì AB = (xB - xA; yB - yA).
- Tích vô hướng của hai vectơ:a . b = xaxb + yayb.
- Điều kiện vuông góc: Hai vectơ a và b vuông góc khi và chỉ khi a . b = 0.
- Điều kiện điểm nằm trên đường thẳng: Điểm M(xM; yM) nằm trên đường thẳng d: ax + by + c = 0 khi và chỉ khi axM + byM + c = 0.
Ví dụ: Giả sử A(1; 2), B(3; 4), C(5; 6). Khi đó:
- AB = (3 - 1; 4 - 2) = (2; 2)
- AC = (5 - 1; 6 - 2) = (4; 4)
- AB . AC = 2*4 + 2*4 = 16
Mẹo giải nhanh
Để giải nhanh bài tập này, học sinh nên:
- Vẽ hình để hình dung rõ hơn về bài toán.
- Sử dụng các công thức một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Bài tập tương tự
Để rèn luyện thêm kỹ năng giải bài tập về vectơ, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 11 tập 1 - Cánh Diều và các tài liệu ôn tập khác.
Kết luận
Bài 6 trang 120 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng. Bằng cách nắm vững các kiến thức cơ bản và rèn luyện kỹ năng giải bài tập, học sinh có thể tự tin giải quyết các bài toán tương tự.
Lưu ý: Đây chỉ là một phần hướng dẫn giải bài tập. Để hiểu rõ hơn về bài tập này, học sinh nên đọc kỹ SGK Toán 11 tập 1 - Cánh Diều và tham khảo các tài liệu ôn tập khác.
| Công thức | Mô tả |
|---|---|
| AB = (xB - xA; yB - yA) | Tọa độ của vectơ AB |
| a . b = xaxb + yayb | Tích vô hướng của hai vectơ a và b |