Bài 2 trang 115 Toán 11 Tập 2 - Cánh Diều | Giải chi tiết & Chính xác

Bài 2 trang 115 SGK Toán 11 tập 2 - Cánh Diều

Bài 2 trang 115 SGK Toán 11 Tập 2 - Cánh Diều

Bài 2 thuộc chương trình học Toán 11 Tập 2, sách Cánh Diều, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này giúp học sinh củng cố kiến thức đã học và phát triển tư duy logic.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững phương pháp giải và tự tin làm bài tập.

Cho hình chóp đều \(S.ABCD\) có các cạnh bên và các cạnh đáy đều bằng \(a\).

Đề bài

Cho hình chóp đều \(S.ABCD\) có các cạnh bên và các cạnh đáy đều bằng \(a\).

a) Chứng minh rằng các tam giác \(ASC\) và \(BSD\) là tam giác vuông cân.

b) Gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\), chứng minh rằng đường thẳng \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\).

c) Chứng minh rằng góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^ \circ }\).

Phương pháp giải - Xem chi tiết Bài 2 trang 115 SGK Toán 11 tập 2 - Cánh Diều 1

a) Chứng minh tam giác có 2 cạnh bằng nhau và có một góc vuông.

b) Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

c) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Lời giải chi tiết

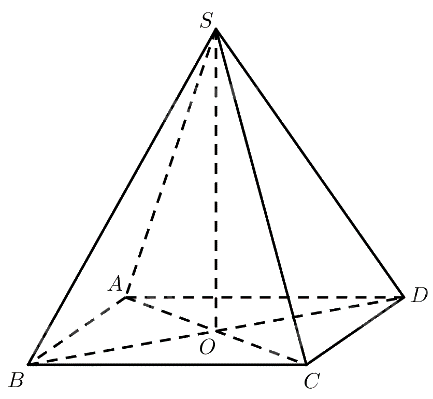
Bài 2 trang 115 SGK Toán 11 tập 2 - Cánh Diều 2

a) \(ABCD\) là hình vuông \( \Rightarrow AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)

Xét \(\Delta ASC\) có: \(S{A^2} + S{C^2} = 2{a^2} = A{C^2},SA = SC\)

Vậy tam giác \(ASC\) là tam giác vuông cân tại \(S\).

Xét \(\Delta BSD\) có: \(S{B^2} + S{D^2} = 2{a^2} = B{{\rm{D}}^2},SB = SD\)

Vậy tam giác \(BSD\) là tam giác vuông cân tại \(S\).

b) \(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow SO \bot AC\)

\(\Delta BSD\) vuông cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)

\( \Rightarrow SO \bot \left( {ABCD} \right)\)

c) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)

\(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow \widehat {SAO} = {45^ \circ }\)

Vậy \(\left( {SA,\left( {ABCD} \right)} \right) = {45^ \circ }\).

Giải Bài 2 trang 115 SGK Toán 11 Tập 2 - Cánh Diều Chi Tiết

Bài 2 trang 115 SGK Toán 11 Tập 2 - Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết cho từng phần của bài tập:

Phần 1: Đề bài

(Giả sử đề bài là: Cho hàm số y = f(x) = x³ - 3x² + 2. Hãy tìm các điểm cực trị của hàm số.)

Phần 2: Lời giải

Bước 1: Tính đạo hàm cấp nhất f'(x)

f'(x) = 3x² - 6x

Bước 2: Tìm các điểm làm đạo hàm bằng 0

3x² - 6x = 0 ⇔ 3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2

Bước 3: Lập bảng xét dấu f'(x)

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	↗	↘	↗

Giải thích:

Khi x < 0, f'(x) > 0, hàm số đồng biến.
Khi 0 < x < 2, f'(x) < 0, hàm số nghịch biến.
Khi x > 2, f'(x) > 0, hàm số đồng biến.

Bước 4: Kết luận

Dựa vào bảng xét dấu, ta thấy:

Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

Phần 3: Lưu ý khi giải bài tập

Khi giải các bài toán về cực trị hàm số, cần lưu ý:

Tính đạo hàm cấp nhất chính xác.
Tìm đúng các điểm làm đạo hàm bằng 0 hoặc không xác định.
Lập bảng xét dấu đạo hàm một cách cẩn thận để xác định khoảng đồng biến, nghịch biến của hàm số.
Kết luận đúng về điểm cực đại, cực tiểu và giá trị tương ứng.

Phần 4: Mở rộng kiến thức

Để hiểu sâu hơn về ứng dụng của đạo hàm trong việc khảo sát hàm số, các em có thể tham khảo thêm:

Các bài tập tương tự trong SGK và sách bài tập.
Các video hướng dẫn giải bài tập trên các trang web học trực tuyến.
Hỏi thầy cô giáo hoặc bạn bè để được giải đáp thắc mắc.

tusach.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 11 Tập 2 - Cánh Diều. Chúc các em học tốt!

(Lưu ý: Nội dung bài viết trên chỉ là ví dụ minh họa. Đề bài và lời giải cụ thể sẽ khác nhau tùy thuộc vào từng bài tập.)