Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều
SGK Toán 11 - Cánh diều
Toán 11 tập 1 - Cánh Diều
Chương 1 Hàm số lượng giác và phương trình lượng giác
Bài 4. Phương trình lượng giác cơ bản

Giải mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều

Giải mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.

Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn bộ giải bài tập Toán 11 tập 1 - Cánh Diều đầy đủ và chính xác.

a) Đường thẳng (d:y = frac{1}{2}) cắt đồ thị hàm số (y = cos x,x in left[ { - pi ;pi } right]) tại hai giao điểm ({C_0},{D_0}) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm ({C_0},{D_0}).

HĐ 4LT - VD 5LT - VD 6

HĐ 4

    a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({C_0},{D_0}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_0},{D_0}\).

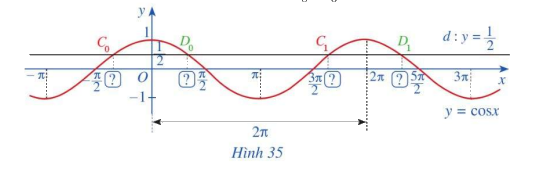
    Giải mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều 1

    b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({C_1},{D_1}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_1},{D_1}\).

    Phương pháp giải:

    Dựa vào kiến thức đã học về lượng giác để xác định tọa độ giao điểm

    Lời giải chi tiết:

    a) Hoành độ của \({C_0}\) là \( - \frac{\pi }{3}\)

    Hoành độ của \({D_0}\) là \(\frac{\pi }{3}\)

    b) Hoành độ của \({C_1}\) là \(\frac{{5\pi }}{3}\)

    Hoành độ của \({D_1}\) là \(\frac{{7\pi }}{3}\)

    LT - VD 5

      a) Giải phương trình \(\cos x = - \frac{1}{2}\)

      b) Tìm góc lượng giác x sao cho \(\cos x = \cos \left( { - {{87}^ \circ }} \right)\)

      Phương pháp giải:

      Sử dụng công thức tổng quát của phương trình cos

      Lời giải chi tiết:

      a) \(\cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \left( {\frac{{2\pi }}{3}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)

      b) \(\cos x = \cos \left( { - {{87}^ \circ }} \right) \Leftrightarrow \left[ \begin{array}{l}x = - {87^ \circ } + k.360\\x = {87^ \circ } + k{.360^ \circ }\end{array} \right.\)

      LT - VD 6

        Giải phương trình được nêu trong bài toán mở đầu.

        Phương pháp giải:

        Sử dụng công thức tổng quát của phương trình cos

        Lời giải chi tiết:

        +) Vệ tinh cách mặt đất 1 000 km thì h=1 000

        Khi đó

         \(\begin{array}{l}1000 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos 0\\ \Leftrightarrow \frac{\pi }{{50}}t = 0 + k2\pi \\ \Leftrightarrow t = 100.k\,\,\,\,;k \in N*\end{array}\)

        +) Vệ tinh cách mặt đất 250 km thì h=250

        Khi đó

         \(\begin{array}{l}250 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = - \frac{2}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{50}}t = \arccos \left( { - \frac{2}{3}} \right) + k2\pi \\\frac{\pi }{{50}}t = - \arccos \left( { - \frac{2}{3}} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{50}}{\pi }\left[ {\arccos \left( { - \frac{2}{3}} \right) + k2\pi } \right]\\t = \frac{{50}}{\pi }\left[ { - \arccos \left( { - \frac{2}{3}} \right) + k2\pi } \right]\end{array} \right.;k \in N*\end{array}\)

        +) Vệ tinh cách mặt đất 100 km thì h=100

        Khi đó

        \(\begin{array}{l}100 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = - 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos \pi \\ \Leftrightarrow \frac{\pi }{{50}}t = \pi + k2\pi \\ \Leftrightarrow t = 50 + 100k\,\,\,\,;k \in N*\end{array}\)

        Giải mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu

        Mục 3 trong SGK Toán 11 tập 1 - Cánh Diều tập trung vào các kiến thức về véc tơ trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học không gian phức tạp hơn trong chương trình học. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.

        Nội dung chính của Mục 3

        • Khái niệm về véc tơ trong không gian: Định nghĩa, các ký hiệu, các phép toán cơ bản (cộng, trừ, nhân với một số).
        • Các tính chất của véc tơ trong không gian: Tính chất giao hoán, kết hợp, phân phối của phép cộng véc tơ, tính chất của phép nhân véc tơ với một số.
        • Hệ tọa độ trong không gian: Cách xác định tọa độ của một điểm và một véc tơ trong không gian.
        • Các phép toán véc tơ trong hệ tọa độ: Công thức tính tổng, hiệu, tích của hai véc tơ trong hệ tọa độ.
        • Ứng dụng của véc tơ trong không gian: Giải các bài toán về hình học không gian, chứng minh các đẳng thức véc tơ.

        Giải chi tiết các bài tập trang 35, 36, 37

        Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều:

        Bài 1: (Trang 35)

        Đề bài: Cho hai điểm A(1; 2; 3) và B(4; 5; 6). Tìm tọa độ của véc tơ AB.

        Lời giải: Véc tơ AB có tọa độ là (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3).

        Bài 2: (Trang 36)

        Đề bài: Cho véc tơ a = (1; -2; 3) và b = (2; 1; -1). Tính véc tơ a + b.

        Lời giải: Véc tơ a + b có tọa độ là (1 + 2; -2 + 1; 3 - 1) = (3; -1; 2).

        Bài 3: (Trang 37)

        Đề bài: Chứng minh rằng nếu a = b thì a - b = 0.

        Lời giải: Nếu a = b thì a - b = a - a = 0 (theo tính chất của phép trừ véc tơ).

        Mẹo giải bài tập véc tơ trong không gian

        • Nắm vững định nghĩa và các tính chất của véc tơ: Đây là nền tảng để giải quyết mọi bài tập liên quan đến véc tơ.
        • Sử dụng hệ tọa độ một cách linh hoạt: Việc biểu diễn véc tơ bằng tọa độ giúp đơn giản hóa các phép toán và chứng minh.
        • Vận dụng các công thức một cách chính xác: Đảm bảo rằng bạn hiểu rõ và áp dụng đúng các công thức tính tổng, hiệu, tích của hai véc tơ.
        • Vẽ hình minh họa: Việc vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.

        Tại sao nên chọn tusach.vn để học Toán 11?

        tusach.vn là địa chỉ tin cậy cho các em học sinh muốn tìm kiếm lời giải bài tập Toán 11 nhanh chóng, chính xác và dễ hiểu. Chúng tôi cung cấp:

        • Lời giải chi tiết, đầy đủ: Giải thích từng bước, giúp các em hiểu rõ bản chất của bài toán.
        • Đội ngũ giáo viên giàu kinh nghiệm: Đảm bảo tính chính xác và chất lượng của lời giải.
        • Giao diện thân thiện, dễ sử dụng: Giúp các em dễ dàng tìm kiếm và học tập.
        • Cập nhật liên tục: Cung cấp lời giải cho tất cả các bài tập trong SGK Toán 11 tập 1 - Cánh Diều.

        Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kết quả học tập của bạn!

        Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

        CHỦ ĐỀ SÁCH XEM NHIỀU

        Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

        VỀ TUSACH.VN