Giải mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Giải mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 - Cánh Diều. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài giải mục 4 trang 37 tập trung vào các kiến thức trọng tâm của chương, giúp bạn nắm vững lý thuyết và áp dụng vào thực tế.
Quan sát giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m (Hình 36).
HĐ 5
Quan sát giao điểm của đồ thị hàm số y = tan x và đường thẳng y = 1
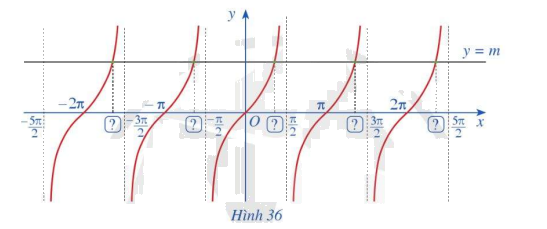
a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó
b) Có nhận xét gì về nghiệm của phương trình tanx = 1
Phương pháp giải:
Dựa vào phương trình lượng giác của sinx và cosx để làm bài
Lời giải chi tiết:
a) Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên: \(\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)
LT - VD 7
a) Giải phương trình \(\tan x = 1\)
b) Tìm góc lượng giác x saoo cho \(\tan x = \tan {67^ \circ }\)
Phương pháp giải:
Sử dụng công thức tổng quát để giải phương trình tan
Lời giải chi tiết:
a) \(\tan x = 1 \Leftrightarrow \tan x = \tan \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
b) \(\tan x = \tan {67^ \circ } \Leftrightarrow x = {67^ \circ } + k{.180^ \circ }\)
Giải mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và hướng dẫn chi tiết
Mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để giúp các em học sinh hiểu rõ hơn về nội dung này, tusach.vn xin giới thiệu bài viết giải chi tiết các bài tập trong mục này.
Nội dung chính của Mục 4 trang 37
Mục 4 trang 37 thường bao gồm các dạng bài tập sau:
- Xác định các hệ số a, b, c của hàm số bậc hai.
- Tìm tập xác định của hàm số bậc hai.
- Xác định đỉnh, trục đối xứng và các điểm đặc biệt của parabol.
- Vẽ đồ thị hàm số bậc hai.
- Giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều:
Bài 1: Xác định hệ số a, b, c
Để xác định hệ số a, b, c của hàm số bậc hai, các em cần đưa hàm số về dạng tổng quát: y = ax2 + bx + c. Sau đó, so sánh với dạng tổng quát để xác định các hệ số.
Ví dụ: Cho hàm số y = 2x2 - 3x + 1. Ta có a = 2, b = -3, c = 1.
Bài 2: Tìm tập xác định
Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x sao cho biểu thức trong hàm số có nghĩa. Thông thường, tập xác định của hàm số bậc hai là tập R (tập hợp tất cả các số thực).
Bài 3: Xác định đỉnh, trục đối xứng
Đỉnh của parabol là điểm có tọa độ (x0, y0), trong đó x0 = -b/2a và y0 = f(x0). Trục đối xứng của parabol là đường thẳng x = x0.
Mẹo giải nhanh
Để giải nhanh các bài tập về hàm số bậc hai, các em có thể áp dụng các công thức và tính chất sau:
- Công thức tính đỉnh: x0 = -b/2a
- Công thức tính trục đối xứng: x = x0
- Nếu a > 0 thì parabol có dạng chữ U, đỉnh là điểm thấp nhất.
- Nếu a < 0 thì parabol có dạng chữ ∩, đỉnh là điểm cao nhất.
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học trực tuyến.
Kết luận
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Mục 4 trang 37 SGK Toán 11 tập 1 - Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định hệ số | Đưa về dạng tổng quát y = ax2 + bx + c |
| Tìm tập xác định | Xác định điều kiện để biểu thức có nghĩa |
| Xác định đỉnh, trục đối xứng | Sử dụng công thức x0 = -b/2a và y0 = f(x0) |