Giải mục 3 trang 108, 109 SGK Toán 11 tập 1 - Cánh Diều
Tổng quan nội dung
Giải mục 3 trang 108, 109 SGK Toán 11 tập 1 - Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 108, 109 SGK Toán 11 tập 1 chương trình Cánh Diều. Bài viết này sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.
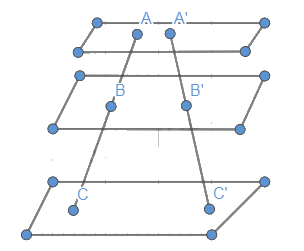
Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi \({B_1}\) là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).
Hoạt động 5
Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi \({B_1}\) là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).
a) Nêu vị trí tương đối của \(B{B_1}\) và \(CC'\);\({B_1}B\) và \(AA'\)
b) Có nhận xét gì về các tỉ số:
\(\frac{{AB}}{{A{B_1}}}, \frac{{BC}}{{{B_1}C'}}\) và \(\frac{{CA}}{{C'A'}}; \frac{{A{B_1}}}{{A'B'}},\frac{{{B_1}C'}}{{B'C'}}\) và \(\frac{{C'A}}{{C'A'}}\)
c) Từ kết quả câu a) và câu b:, so sánh các tỉ số:
\(\frac{{AB}}{{A'B'}},\frac{{BC}}{{B'C'}}\)và\(\frac{{CA}}{{C'A'}}\)
Phương pháp giải:
Định lý Ta-let:
Nếu a, b là hai cát tuyến bất kỳ cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
Lời giải chi tiết:
a) \(B{B_1}\)và\(CC'\)song song với nhau
\({B_1}B\)và\(AA'\)song song với nhau
b) Các tỉ số:
\(\frac{{AB}}{{A{B_1}}} = \frac{{BC}}{{{B_1}C'}} = \frac{{CA}}{{C'A'}}\)
\(\frac{{A{B_1}}}{{A'B'}} = \frac{{{B_1}C'}}{{B'C'}} = \frac{{C'A}}{{C'A'}}\)
c) Các tỉ số:\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
Luyện tập 4
Bạn Minh cho rằng: Nếu a, b là cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
Phát biểu của bạn Minh có đúng không? Vì sao?

Phương pháp giải:
Nếu a,b là hai cát tuyến bất kì cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A,B, C và A’, B’, C’ thì
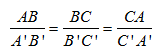
Lời giải chi tiết:
Bạn Minh phát biểu sai vì \(\frac{{CA}}{{C'A'}} = \frac{{AB + BC}}{{A'B' + B'C'}} \ne \frac{{AB}}{{BC}} \ne \frac{{A'B'}}{{B'C'}}\)
Giải mục 3 trang 108, 109 SGK Toán 11 tập 1 - Cánh Diều: Tổng quan và Phương pháp giải
Mục 3 trang 108, 109 SGK Toán 11 tập 1 chương trình Cánh Diều tập trung vào việc ôn tập chương 1: Hàm số lượng giác và đồ thị. Đây là một phần quan trọng trong chương trình Toán 11, đặt nền móng cho các kiến thức nâng cao hơn. Việc nắm vững các khái niệm và phương pháp giải bài tập trong mục này là vô cùng cần thiết để đạt kết quả tốt trong các bài kiểm tra và kỳ thi sắp tới.
Nội dung chính của Mục 3
Mục 3 bao gồm các dạng bài tập sau:
- Bài tập về xác định tập xác định của hàm số lượng giác: Các bài tập này yêu cầu học sinh phải nắm vững điều kiện xác định của các hàm số lượng giác (sin, cos, tan, cot) và áp dụng vào giải bài tập cụ thể.
- Bài tập về xét tính chẵn lẻ của hàm số lượng giác: Học sinh cần hiểu rõ định nghĩa về hàm số chẵn, hàm số lẻ và sử dụng các tính chất của hàm số lượng giác để xét tính chẵn lẻ.
- Bài tập về tìm chu kỳ của hàm số lượng giác: Việc tìm chu kỳ của hàm số lượng giác giúp học sinh hiểu rõ hơn về tính tuần hoàn của hàm số và ứng dụng vào giải các bài toán liên quan.
- Bài tập về vẽ đồ thị hàm số lượng giác: Học sinh cần nắm vững các bước vẽ đồ thị hàm số lượng giác và sử dụng các phép biến đổi đồ thị để vẽ đồ thị của các hàm số phức tạp hơn.
Hướng dẫn giải chi tiết các bài tập
Bài 1: Xác định tập xác định của hàm số y = tan(2x + π/3)
Để xác định tập xác định của hàm số y = tan(2x + π/3), ta cần tìm các giá trị của x sao cho 2x + π/3 ≠ π/2 + kπ (k ∈ Z). Giải phương trình này, ta được x ≠ π/12 + kπ/2 (k ∈ Z). Vậy tập xác định của hàm số là D = R \ {π/12 + kπ/2 | k ∈ Z}.
Bài 2: Xét tính chẵn lẻ của hàm số y = sin2x + cos x
Để xét tính chẵn lẻ của hàm số y = sin2x + cos x, ta tính y(-x) = sin2(-x) + cos(-x) = sin2x + cos x = y(x). Vì y(-x) = y(x) với mọi x thuộc tập xác định, nên hàm số y = sin2x + cos x là hàm số chẵn.
Bài 3: Tìm chu kỳ của hàm số y = 3cos(2x - π/4)
Chu kỳ của hàm số y = cos x là T = 2π. Chu kỳ của hàm số y = cos(ax + b) là T' = 2π/|a|. Trong trường hợp này, a = 2, nên chu kỳ của hàm số y = 3cos(2x - π/4) là T' = 2π/2 = π.
Mẹo giải nhanh và hiệu quả
Để giải các bài tập về hàm số lượng giác một cách nhanh chóng và hiệu quả, các em nên:
- Nắm vững các công thức lượng giác cơ bản.
- Sử dụng các phép biến đổi lượng giác để đơn giản hóa biểu thức.
- Vẽ đồ thị hàm số để hình dung rõ hơn về tính chất của hàm số.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tài liệu tham khảo hữu ích
Ngoài SGK Toán 11 tập 1 Cánh Diều, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Các video bài giảng Toán 11 trên YouTube
Kết luận
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn khi giải các bài tập mục 3 trang 108, 109 SGK Toán 11 tập 1 chương trình Cánh Diều. Chúc các em học tập tốt!