Giải câu hỏi trắc nghiệm trang 160 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải Câu Hỏi Trắc Nghiệm Toán 11 Trang 160 - Chân Trời Sáng Tạo Tập 1
Bạn đang gặp khó khăn trong việc giải các bài tập trắc nghiệm Toán 11 trang 160 sách bài tập Chân Trời Sáng Tạo Tập 1? Đừng lo lắng, tusach.vn sẽ giúp bạn! Chúng tôi cung cấp đáp án chi tiết, dễ hiểu và phương pháp giải bài tập hiệu quả.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất.
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây. Tổng số học sinh tham gia kì thi đánh giá năng lực trên là A. 780. B. 787. C. 696. D. 697.
Câu 1
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
Tổng số học sinh tham gia kì thi đánh giá năng lực trên là
A. 780.
B. 787.
C. 696.
D. 697.
Phương pháp giải:
Để tính tổng số học sinh tham gia kì thi, đếm xem mỗi khoảng điểm có bao nhiêu học sinh tham gia, rồi cộng tổng lại.
Lời giải chi tiết:
Tổng số học sinh tham gia kì thi đánh giá năng lực là:
\(1 + 8 + 24 + 54 + 95 + 95 + 133 + 122 + 104 + 62 + 55 + 21 + 12 + 1 = 787\) (học sinh)
Chọn B
Câu 2
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa mốt của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Sử dụng kiến thức về nhóm chứa một của mẫu số liệu để tính: Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:
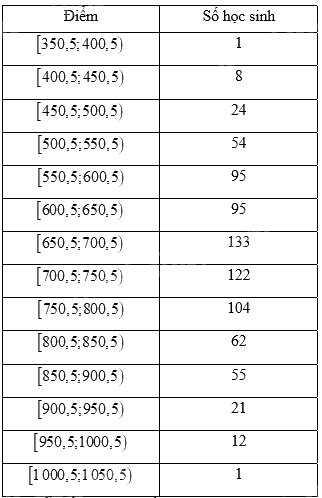
Nhóm chứa mốt của mẫu số liệu ghép nhóm là \(\left[ {650,5;700,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {650,5;700,5} \right)\) là: \(\frac{1}{2}\left( {650,5 + 700,5} \right) = 675,5\)
Chọn B.
Câu 3
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa trung vị của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa trung vị, ta đi tìm trung vị của mẫu số liệu rồi xét xem trung vị đó thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:

Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Vì \(n = 787\) nên trung vị của mẫu số liệu là \({x_{394}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {650,5;700,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {650,5;700,5} \right)\) là: \(\frac{1}{2}\left( {650,5 + 700,5} \right) = 675,5\)
Chọn B
Câu 4
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa tứ phân vị thứ nhất, ta đi tìm tứ phân vị thứ nhất rồi xét xem t tứ phân vị thứ nhất thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:

Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu là \({x_{197}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {600,5;650,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {600,5;650,5} \right)\) là: \(\frac{1}{2}\left( {600,5 + 650,5} \right) = 625,5\)
Chọn A
Câu 5
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa tứ phân vị thứ ba, ta đi tìm tứ phân vị thứ ba rồi xét xem tứ phân vị thứ ba thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:

Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ ba của mẫu số liệu là \({x_{591}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {750,5;800,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {750,5;800,5} \right)\) là: \(\frac{1}{2}\left( {750,5 + 800,5} \right) = 775,5\)
Chọn D
Câu 6
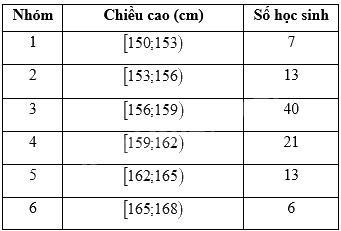
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

160,5 là giá trị đại diện cho nhóm
A. 2.
B. 3.
C. 4.
D. 5.
Phương pháp giải:
Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
Lời giải chi tiết:
Giá trị đại diện của nhóm \(\left[ {159;162} \right)\) là: \(\frac{1}{2}\left( {159 + 162} \right) = 160,5\)
Vậy 160,5 là giá trị đại diện cho nhóm 4.
Chọn C
Câu 7
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 157,76.
B. 158,25.
C. 157,5.
D. 160,28.
Phương pháp giải:
Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Lời giải chi tiết:
Nhóm chứa mốt của mẫu số liệu là nhóm \(\left[ {156;159} \right)\).
Do đó, \({u_m} = 156,{n_{m - 1}} = 13,{n_m} = 40,{n_{m + 1}} = 21,{u_{m + 1}} = 159\)
Mốt của mẫu số liệu trên là:
\({M_O} = 156 + \frac{{40 - 13}}{{\left( {40 - 13} \right) + \left( {40 - 21} \right)}}.\left( {159 - 156} \right) \approx 157,76\)
Chọn A
Câu 8
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Trung vị của mẫu số liệu ghép nhóm trên là
A. 157,76.
B. 157,25.
C. 158,25.
D. 160,45.
Phương pháp giải:
Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên trung vị của mẫu số liệu là \(\frac{{{x_{50}} + {x_{51}}}}{2}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Trung vị của mẫu số liệu ghép nhóm là: \({M_e} = 156 + \frac{{\frac{{100}}{2} - \left( {7 + 13} \right)}}{{40}}.\left( {159 - 156} \right) = 158,25\)
Chọn C
Câu 9
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 156,25.
B. 157,5.
C. 156,38.
D. 157,54.
Phương pháp giải:
Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{{{x_{25}} + {x_{26}}}}{2}\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 156 + \frac{{\frac{{100}}{4} - \left( {7 + 13} \right)}}{{40}}.\left( {159 - 156} \right) = 156,375 \approx 156,38\)
Chọn C
Câu 10
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 160,52.
B. 161,52.
C. 161,14.
D. 162,25.
Phương pháp giải:
Sử dụng kiến thức về tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{{{x_{75}} + {x_{76}}}}{2}\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {159;162} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 159 + \frac{{\frac{{3.100}}{4} - \left( {7 + 13 + 40} \right)}}{{21}}.\left( {162 - 159} \right) \approx 161,14\)
Chọn C
Giải Chi Tiết Câu Hỏi Trắc Nghiệm Toán 11 Trang 160 - Chân Trời Sáng Tạo Tập 1
Trang 160 sách bài tập Toán 11 Chân Trời Sáng Tạo Tập 1 tập trung vào các chủ đề về hàm số lượng giác, bao gồm các dạng bài tập về tập xác định, tập giá trị, tính đơn điệu, cực trị và ứng dụng của hàm số lượng giác. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Tổng Quan Về Hàm Số Lượng Giác
Hàm số lượng giác là một trong những chủ đề quan trọng trong chương trình Toán 11. Các hàm số lượng giác cơ bản bao gồm sin, cos, tan và cot. Hiểu rõ tính chất của từng hàm số, như tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, là bước đầu tiên để giải quyết các bài tập liên quan.
Các Dạng Bài Tập Trắc Nghiệm Thường Gặp
- Xác định tập xác định của hàm số: Bài tập này yêu cầu học sinh phải xác định được các giá trị của x sao cho hàm số có nghĩa.
- Tìm tập giá trị của hàm số: Học sinh cần xác định khoảng giá trị mà hàm số có thể đạt được.
- Xác định tính đơn điệu của hàm số: Bài tập này yêu cầu học sinh phải xét dấu đạo hàm của hàm số để xác định khoảng tăng, khoảng giảm.
- Tìm cực trị của hàm số: Học sinh cần tìm các điểm mà hàm số đạt cực đại hoặc cực tiểu.
- Ứng dụng hàm số lượng giác vào giải quyết bài toán thực tế: Các bài toán này thường liên quan đến việc mô tả các hiện tượng vật lý hoặc hình học bằng hàm số lượng giác.
Hướng Dẫn Giải Chi Tiết Một Số Bài Tập Ví Dụ
Ví dụ 1: Tìm tập xác định của hàm số y = tan(2x).
Giải: Hàm số y = tan(2x) xác định khi và chỉ khi cos(2x) ≠ 0. Điều này tương đương với 2x ≠ π/2 + kπ, với k là số nguyên. Suy ra x ≠ π/4 + kπ/2, với k là số nguyên. Vậy tập xác định của hàm số là D = R \ {π/4 + kπ/2, k ∈ Z}.
Ví dụ 2: Tìm giá trị lớn nhất của hàm số y = 2sin(x) + 1.
Giải: Vì -1 ≤ sin(x) ≤ 1, nên -2 ≤ 2sin(x) ≤ 2. Do đó, -1 ≤ 2sin(x) + 1 ≤ 3. Vậy giá trị lớn nhất của hàm số là 3, đạt được khi sin(x) = 1.
Mẹo Giải Bài Tập Trắc Nghiệm Toán 11 Hiệu Quả
- Nắm vững kiến thức lý thuyết: Đây là nền tảng quan trọng để giải quyết mọi bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn làm quen với các dạng bài và rèn luyện kỹ năng giải quyết vấn đề.
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn tự hào là một trong những trang web cung cấp tài liệu học tập và giải bài tập Toán 11 uy tín và chất lượng. Chúng tôi luôn cập nhật những thông tin mới nhất và cung cấp những giải pháp học tập hiệu quả nhất cho học sinh. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Chúng tôi hy vọng rằng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, bạn sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm Toán 11 trang 160 sách bài tập Chân Trời Sáng Tạo Tập 1. Chúc bạn học tập tốt!