Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 3 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2
SBT Toán 11 - Chân trời sáng tạo
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Chương 8. Quan hệ vuông góc trong không gian
Bài 4. Khoảng cách trong không gian

Giải bài 3 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 3 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2

Tusach.vn xin giới thiệu lời giải chi tiết bài 3 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.

Chúng tôi luôn cập nhật lời giải nhanh chóng và chính xác nhất, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.

Phương pháp giải - Xem chi tiếtGiải bài 3 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 1

Sử dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau để tính: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b).

Lời giải chi tiết

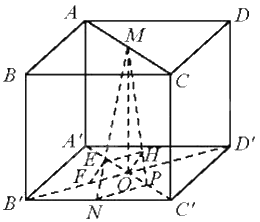
Giải bài 3 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 2

Gọi O là giao điểm của B’D’ và A’C’. Gọi P là trung điểm của OC’.

Vẽ \(OH \bot MP,HE//NP,EF//OH\) (H thuộc MP, E thuộc MN, F thuộc B’D’)

Chứng minh được \(B'D' \bot \left( {A'C'CA} \right)\) nên \(B'D' \bot OH\), mà \(EF//OH\) nên \(EF \bot B'D'\left( 1 \right)\)

Vì NP//B’D’ nên \(NP \bot \left( {A'C'CA} \right) \Rightarrow NP \bot OH\), mà \(OH \bot MP\) nên \(OH \bot \left( {MNP} \right)\) hay \(OH \bot MN\), mà \(EF//OH\)\( \Rightarrow EF \bot MN\left( 2 \right)\)

Từ (1) và (2) ta có: \(d\left( {MN,B'D'} \right) = EF = OH\)

Tam giác MOP vuông tại O, ta có: \(OM = a,OP = \frac{1}{2}OC' = \frac{1}{4}A'C' = \frac{{a\sqrt 2 }}{4}\) nên

\(\frac{1}{{O{H^2}}} = \frac{1}{{O{P^2}}} + \frac{1}{{O{M^2}}} = {\left( {\frac{4}{{a\sqrt 2 }}} \right)^2} + \frac{1}{{{a^2}}} = \frac{9}{{{a^2}}}\)\( \Rightarrow OH = \frac{a}{3}\)

Giải bài 3 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2: Tổng quan và Phương pháp giải

Bài 3 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về Đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).

Nội dung chi tiết bài 3 trang 68

Để giải quyết bài 3 trang 68 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

  • Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và đạo hàm của hàm số.
  • Các quy tắc tính đạo hàm:
    • Đạo hàm của hàm số lũy thừa: (xn)' = nxn-1
    • Đạo hàm của hàm số lượng giác: (sin x)' = cos x, (cos x)' = -sin x, ...
    • Đạo hàm của hàm số mũ và logarit: (ex)' = ex, (ln x)' = 1/x, ...
    • Quy tắc đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
  • Ứng dụng của đạo hàm: Tìm đạo hàm để giải các bài toán liên quan đến tiếp tuyến, vận tốc, gia tốc,...

Lời giải chi tiết bài 3 trang 68 (Ví dụ)

(Giả sử bài 3 yêu cầu tính đạo hàm của hàm số f(x) = 2x3 - 5x2 + 7x - 3)

Lời giải:

Áp dụng quy tắc đạo hàm của hàm đa thức, ta có:

f'(x) = (2x3)' - (5x2)' + (7x)' - (3)'

f'(x) = 6x2 - 10x + 7 - 0

f'(x) = 6x2 - 10x + 7

Các dạng bài tập thường gặp trong bài 3 trang 68

  1. Tính đạo hàm của hàm số đơn giản: Hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
  2. Tính đạo hàm của hàm số phức tạp: Sử dụng quy tắc đạo hàm của hàm hợp, tích, thương.
  3. Tìm đạo hàm cấp hai: Tính đạo hàm của đạo hàm cấp một.
  4. Ứng dụng đạo hàm để giải các bài toán thực tế: Tìm tiếp tuyến, vận tốc, gia tốc.

Mẹo giải bài tập đạo hàm hiệu quả

  • Nắm vững các quy tắc tính đạo hàm: Đây là nền tảng quan trọng nhất để giải quyết các bài tập.
  • Phân tích cấu trúc hàm số: Xác định hàm số thuộc loại nào (đa thức, lượng giác, mũ, logarit, hàm hợp,...) để áp dụng quy tắc phù hợp.
  • Thực hành thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
  • Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả bằng cách thay các giá trị cụ thể của x vào hàm số và đạo hàm để đảm bảo tính chính xác.

Tusach.vn - Hỗ trợ học tập Toán 11 hiệu quả

Tusach.vn cung cấp đầy đủ lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong Sách bài tập Toán 11 Chân trời sáng tạo tập 2. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.

Ngoài ra, bạn có thể tham khảo thêm các tài liệu học tập khác như lý thuyết, công thức, bài tập trắc nghiệm và video bài giảng tại Tusach.vn.

Chúc bạn học tập tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN