Giải bài 3 trang 55 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Tổng quan nội dung
Giải bài 3 trang 55 SBT Toán 11 Chân trời sáng tạo tập 2
Bài 3 trang 55 SBT Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, bám sát chương trình học, giúp các em học sinh tự tin giải quyết bài tập và nâng cao kết quả học tập.
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ \(AH \bot MD\) tại H.
Đề bài
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ \(AH \bot MD\) tại H.
a) Chứng minh rằng \(AH \bot \left( {BCD} \right)\).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng \(GK \bot \left( {ABC} \right)\).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lí đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải chi tiết
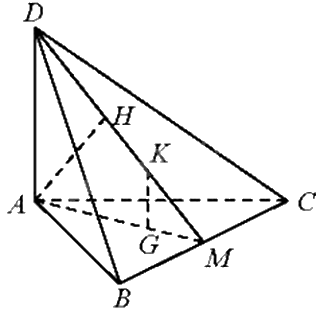
a) Vì \(DA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow DA \bot BC\)
Tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao, suy ra: \(BC \bot AM\)
Vì \(DA \bot BC\), \(BC \bot AM\), DA và AM cắt nhau tại A và nằm trong (DAM) nên \(BC \bot \left( {DAM} \right)\). Lại có, \(AH \subset \left( {DAM} \right) \Rightarrow AH \bot BC\)
Ta có: \(AH \bot MD\), \(AH \bot BC\), MD và BC cắt nhau tại M và nằm trong (BCD) nên \(AH \bot \left( {BCD} \right)\)
b) Tam giác DBC có K là trọng tâm và DM là đường trung tuyến nên \(\frac{{DK}}{{DM}} = \frac{2}{3}\)
Tam giác ABC có G là trọng tâm và AM là đường trung tuyến nên \(\frac{{AG}}{{AM}} = \frac{2}{3}\)
Tam giác ADM có: \(\frac{{DK}}{{DM}} = \frac{{AG}}{{AM}}\left( { = \frac{2}{3}} \right)\) nên KG//AD (định lí Thalès đảo)
Mà \(DA \bot \left( {ABC} \right)\) nên \(GK \bot \left( {ABC} \right)\).
Giải bài 3 trang 55 SBT Toán 11 Chân trời sáng tạo tập 2: Hướng dẫn chi tiết và dễ hiểu
Bài 3 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến việc tìm đạo hàm của hàm số và ứng dụng vào việc khảo sát hàm số.
Nội dung bài tập
Bài 3 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số hợp.
- Tìm đạo hàm cấp hai của hàm số.
- Khảo sát hàm số bằng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị).
Lời giải chi tiết bài 3 trang 55 SBT Toán 11 Chân trời sáng tạo tập 2
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, tusach.vn xin trình bày lời giải chi tiết như sau:
(a) Giả sử hàm số cần khảo sát là y = f(x). Để tìm đạo hàm f'(x), ta sử dụng các quy tắc tính đạo hàm đã học, bao gồm quy tắc đạo hàm của tổng, hiệu, tích, thương và quy tắc đạo hàm của hàm hợp.
(b) Để tìm đạo hàm cấp hai f''(x), ta tiếp tục tính đạo hàm của f'(x).
(c) Để khảo sát hàm số, ta thực hiện các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm f'(x).
- Tìm các điểm tới hạn (điểm mà f'(x) = 0 hoặc không xác định).
- Lập bảng biến thiên của f'(x) để xác định khoảng đồng biến, nghịch biến của hàm số.
- Tìm cực trị của hàm số.
- Tính giới hạn của hàm số khi x tiến tới vô cùng và các điểm gián đoạn.
- Vẽ đồ thị hàm số.
Ví dụ minh họa
Giả sử hàm số y = x3 - 3x2 + 2. Ta thực hiện khảo sát hàm số như sau:
| Bước | Nội dung |
|---|---|
| 1 | Tập xác định: D = R |
| 2 | Đạo hàm: y' = 3x2 - 6x |
| 3 | Điểm tới hạn: y' = 0 => x = 0 hoặc x = 2 |
| 4 | Bảng biến thiên: |
| 5 | Cực trị: Điểm cực đại (0, 2), Điểm cực tiểu (2, -2) |
Mẹo giải bài tập
- Nắm vững các quy tắc tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập.
- Sử dụng máy tính cầm tay để kiểm tra kết quả.
- Tham khảo các tài liệu tham khảo và lời giải trên mạng.
Tại sao nên chọn tusach.vn để giải bài tập Toán 11?
tusach.vn là một website uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 11. Chúng tôi có đội ngũ giáo viên giàu kinh nghiệm, luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả. Ngoài ra, tusach.vn còn cung cấp nhiều tài liệu học tập hữu ích khác, giúp các em học sinh học tập tốt hơn.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài 3 trang 55 SBT Toán 11 Chân trời sáng tạo tập 2 và đạt kết quả tốt trong môn Toán.