Giải bài 2 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Tổng quan nội dung
Giải bài 2 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2
Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 73 trong sách bài tập Toán 11 Chân trời sáng tạo tập 2. Chúng tôi sẽ trình bày các bước giải cụ thể, kèm theo giải thích chi tiết để giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm I của cạnh AB.
Đề bài
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm I của cạnh AB. Biết rằng mặt bên (SAB) là tam giác vuông cân tại S. Xác định và tính góc giữa:
a) SA và (ABC);
b) SC và (SAB).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:
+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).
+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P).
Lời giải chi tiết
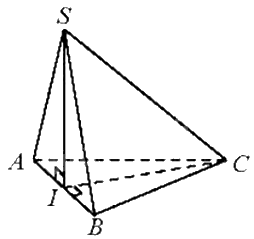
a) Vì \(SI \bot \left( {ABC} \right)\) nên I là hình chiếu của S trên mặt phẳng (ABC).
Do đó, \(\left( {SA,\left( {ABC} \right)} \right) \) \( = \left( {SA,AI} \right) \) \( = \widehat {SAI}\)
Vì tam giác SAB vuông cân tại S nên \(\widehat {SAI} \) \( = {45^0}\)
b) Tam giác ABC đều nên CI là đường trung tuyến đồng thời là đường cao. Do đó, \(IC \bot AB\). Lại có: \(SI \bot IC\left( {do\;SI \bot \left( {ABC} \right)} \right)\) nên \(IC \bot \left( {SAB} \right)\)
Suy ra, I là hình chiếu của C lên mặt phẳng (SAB). Do đó, \(\left( {SC,\left( {SAB} \right)} \right) \) \( = \left( {SC,SI} \right) \) \( = \widehat {CSI}\)
Tam giác ABC đều nên \(IC \) \( = \frac{{AB\sqrt 3 }}{2} \) \( = \frac{{3\sqrt 3 }}{3}\)
Tam giác SAB vuông cân tại S nên SI là đường trung tuyến nên \(SI \) \( = AI \) \( = \frac{1}{2}AB \) \( = \frac{3}{2}\)
Tam giác SIC vuông tại I nên \(\tan \widehat {ISC} \) \( = \frac{{IC}}{{SI}} \) \( = \frac{{\frac{{3\sqrt 3 }}{2}}}{{\frac{3}{2}}} \) \( = \sqrt 3 \) \( \Rightarrow \widehat {ISC} \) \( = {60^0}\)
Giải bài 2 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2: Tổng quan và Phương pháp giải
Bài 2 trang 73 Sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và thực hành thường xuyên là chìa khóa để giải quyết thành công bài tập này.
Nội dung chi tiết bài 2 trang 73
Để giải bài 2 trang 73, chúng ta cần xem xét kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập sẽ yêu cầu:
- Tính đạo hàm của một hàm số cho trước.
- Tìm đạo hàm cấp hai của một hàm số.
- Xác định khoảng đơn điệu của hàm số dựa vào đạo hàm.
- Tìm cực trị của hàm số.
Lời giải chi tiết bài 2 trang 73 (Ví dụ)
Giả sử bài 2 yêu cầu tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1.
- Bước 1: Áp dụng quy tắc đạo hàm của tổng và hiệu: f'(x) = (x3)' - (3x2)' + (2x)' + (1)'
- Bước 2: Áp dụng quy tắc đạo hàm của lũy thừa: (xn)' = nxn-1
- Bước 3: Tính đạo hàm của từng thành phần: (x3)' = 3x2, (3x2)' = 6x, (2x)' = 2, (1)' = 0
- Bước 4: Thay các kết quả vào bước 1: f'(x) = 3x2 - 6x + 2
Vậy, đạo hàm của hàm số f(x) = x3 - 3x2 + 2x + 1 là f'(x) = 3x2 - 6x + 2.
Mẹo giải bài tập đạo hàm hiệu quả
- Nắm vững lý thuyết: Hiểu rõ các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Sử dụng công cụ hỗ trợ: Các công cụ tính đạo hàm trực tuyến có thể giúp bạn kiểm tra kết quả và hiểu rõ hơn về quá trình giải.
Tầm quan trọng của việc giải bài tập đạo hàm
Đạo hàm là một khái niệm quan trọng trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế, và kỹ thuật. Việc nắm vững kiến thức về đạo hàm giúp bạn:
- Giải quyết các bài toán tối ưu hóa.
- Phân tích sự thay đổi của các hàm số.
- Mô tả các hiện tượng vật lý và kinh tế.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn là một website cung cấp đầy đủ và chính xác các lời giải bài tập Toán 11, bao gồm cả sách giáo khoa và sách bài tập Chân trời sáng tạo. Chúng tôi cam kết mang đến cho bạn những tài liệu học tập chất lượng cao, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.
Bảng tổng hợp các công thức đạo hàm thường gặp
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 2 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Chúc bạn học tập tốt!