Giải bài 2 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Tổng quan nội dung
Giải bài 2 trang 61 SBT Toán 11 Chân trời sáng tạo tập 2
Bài 2 trang 61 SBT Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng, cấp số nhân.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, bám sát chương trình học, giúp các em học sinh tự tin giải quyết bài tập và nâng cao kết quả học tập.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết \(SA = a\) và \(SA \bot \left( {ABCD} \right)\).
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết \(SA = a\) và \(SA \bot \left( {ABCD} \right)\). Trên BC lấy điểm I sao cho tam giác SDI vuông tại S. Biết góc giữa hai mặt phẳng (SDI) và (ABCD) là \({60^0}\). Tính độ dài SI.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
Lời giải chi tiết
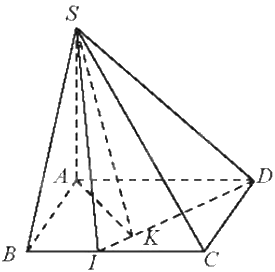
Kẻ \(AK \bot ID\) tại K. Vì \(SA \bot \left( {ABCD} \right),AK \subset \left( {ABCD} \right) \Rightarrow SA \bot ID\), mà \(AK \bot ID\) nên \(ID \bot \left( {SAK} \right) \Rightarrow ID \bot SK\)
Ta có: \(AK \bot ID,ID \bot SK,AK \subset \left( {ABCD} \right),SK \subset \left( {SID} \right)\), ID là giao tuyến của hai mặt phẳng SID và ABCD. Do đó, \(\left( {\left( {SID} \right),\left( {ABCD} \right)} \right) = \left( {SK,AK} \right) = \widehat {SKA} = {60^0}\)
Vì \(SA \bot \left( {ABCD} \right),AD,AK \subset \left( {ABCD} \right) \Rightarrow SA \bot AD,SA \bot AK\)
Áp dụng định lí Pythagore vào tam giác SAD vuông tại A có:
\(SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
Tam giác SAK vuông tại A nên: \(\sin \widehat {SKA} = \frac{{SA}}{{SK}} \Rightarrow SK = \frac{{SA}}{{\sin \widehat {SKA}}} = \frac{{2a\sqrt 3 }}{3}\)
Tam giác SID vuông tại S, đường cao SK có:
\(\frac{1}{{S{I^2}}} + \frac{1}{{S{D^2}}} = \frac{1}{{S{K^2}}} \) \( \Rightarrow \frac{1}{{S{I^2}}} = \frac{1}{{S{K^2}}} - \frac{1}{{S{D^2}}} = \left( {\frac{9}{{12{a^2}}}} \right) - \frac{1}{{{{\left( {a\sqrt 5 } \right)}^2}}} = \frac{{11}}{{20{a^2}}} \) \( \Rightarrow SI = \frac{{2a\sqrt {55} }}{{11}}\)
Giải bài 2 trang 61 SBT Toán 11 Chân trời sáng tạo tập 2: Hướng dẫn chi tiết và dễ hiểu
Bài 2 trang 61 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về dãy số, cấp số cộng và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế liên quan đến dãy số. Dưới đây là hướng dẫn chi tiết từng bước để giải bài 2 trang 61, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài.
Nội dung bài tập
Bài 2 yêu cầu chúng ta tìm số hạng tổng quát của dãy số và tính tổng của một số hạng đầu tiên. Cụ thể, bài tập có thể yêu cầu:
- Tìm số hạng thứ n của một dãy số cho trước.
- Tính tổng của n số hạng đầu tiên của một cấp số cộng hoặc cấp số nhân.
- Xác định các yếu tố của cấp số cộng hoặc cấp số nhân (số hạng đầu, công sai/công bội).
Phương pháp giải
Để giải bài 2 trang 61 SBT Toán 11 Chân trời sáng tạo tập 2, chúng ta cần nắm vững các công thức và phương pháp sau:
- Dãy số: Hiểu rõ khái niệm dãy số, số hạng tổng quát của dãy số.
- Cấp số cộng: Công thức tính số hạng thứ n (un = u1 + (n-1)d), công thức tính tổng n số hạng đầu tiên (Sn = n/2 * (u1 + un) hoặc Sn = n/2 * [2u1 + (n-1)d]).
- Cấp số nhân: Công thức tính số hạng thứ n (un = u1 * qn-1), công thức tính tổng n số hạng đầu tiên (Sn = u1 * (1 - qn) / (1 - q) nếu q ≠ 1).
Lời giải chi tiết
(Ví dụ minh họa - Giả sử bài tập cụ thể là tìm số hạng thứ 10 của cấp số cộng có số hạng đầu u1 = 2 và công sai d = 3)
Áp dụng công thức tính số hạng thứ n của cấp số cộng: un = u1 + (n-1)d
Thay u1 = 2, d = 3 và n = 10 vào công thức, ta có:
u10 = 2 + (10-1) * 3 = 2 + 9 * 3 = 2 + 27 = 29
Vậy số hạng thứ 10 của cấp số cộng là 29.
Lưu ý khi giải bài tập
- Đọc kỹ đề bài để xác định đúng loại dãy số (cấp số cộng, cấp số nhân hay dãy số khác).
- Xác định đúng các yếu tố của dãy số (số hạng đầu, công sai/công bội).
- Sử dụng đúng công thức để tính toán.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong sách bài tập Toán 11 Chân trời sáng tạo tập 2. Ngoài ra, các em có thể tham khảo thêm các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên tusach.vn.
Tại sao nên chọn tusach.vn để học Toán 11?
tusach.vn là một website học tập uy tín, cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm:
- Lời giải chi tiết các bài tập trong sách giáo khoa và sách bài tập.
- Các bài giảng video dễ hiểu, sinh động.
- Các bài kiểm tra trực tuyến giúp các em tự đánh giá kiến thức.
- Đội ngũ giáo viên giàu kinh nghiệm sẵn sàng hỗ trợ các em giải đáp thắc mắc.
Hãy truy cập tusach.vn ngay hôm nay để học Toán 11 hiệu quả và đạt kết quả cao!