Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 \). Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Gọi \(\left( \alpha \right)\) là mặt phẳng qua AB và vuông góc với mặt phẳng (SCD).
a) Tìm các giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
b) Các giao tuyến ở câu a tạo thành hình gì? Tính diện tích của hình đó.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
+ Sử dụng kiến thức về tính chất cơ bản của hai mặt phẳng vuông góc: Nếu hai mặt phẳng vuông góc với nhau mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết
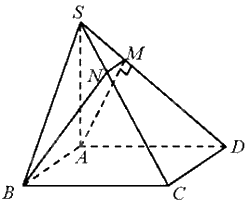
a) Vì mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy, SA là giao tuyến của hai mặt phẳng (SAB) và (SAD) nên \(SA \bot \left( {ABCD} \right)\)
Vì ABCD là hình vuông nên \(AD \bot DC\).
Mà \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \) \( \Rightarrow SA \bot DC\)
Do đó, \(DC \bot \left( {SAD} \right)\). Lại có: \(DC \subset \left( {SDC} \right) \) \( \Rightarrow \left( {SCD} \right) \bot \left( {SAD} \right)\)
Vẽ \(AM \bot SD\) tại M. Do đó, \(AM \bot \left( {SCD} \right)\). Suy ra, \(\left( {BAM} \right) \bot \left( {SCD} \right)\) hay (ABM) là mặt phẳng qua AB và vuông góc với mặt phẳng (SCD).
Trong mặt phẳng (SCD), kẻ MN//CD\(\left( {N \in SC} \right)\). Suy ra, MN//AB nên \(MN \subset \left( \alpha \right)\)
Khi đó, giao tuyến của \(\left( \alpha \right)\) với:
Mặt phẳng (ABCD) là AB.
Mặt phẳng (ABS) là AB.
Mặt phẳng (SBC) là NB.
Mặt phẳng (SCD) là MN.
Mặt phẳng (ASD) là AM.
b) Ta có: MN//AB, \(AB \bot AM\left( {do\;AB \bot \left( {SAD} \right)} \right)\) nên tứ giác ABNM là hình thang vuông tại A và M.
Tam giác SAD vuông tại A có AM là đường cao nên
\(\frac{1}{{A{M^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}} \) \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2}\)
Vì MN//CD nên \(\frac{{MN}}{{CD}} = \frac{{SM}}{{SD}} \) \( \Rightarrow \frac{{MN}}{{CD}} = \frac{{\frac{{S{A^2}}}{{SD}}}}{{SD}} = \frac{{S{A^2}}}{{S{D^2}}} = \frac{{S{A^2}}}{{S{A^2} + A{D^2}}} = \frac{{3{a^2}}}{{4{a^2}}} = \frac{3}{4}\)
Do đó, \(MN = \frac{3}{4}CD = \frac{3}{4}a\)
Vậy diện tích hình thang ABNM là: \(S = \frac{1}{2}AM\left( {MN + AB} \right) \) \(= \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.\left( {\frac{3}{4}a + a} \right) = \frac{{7{a^2}\sqrt 3 }}{{16}}\)
