Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 4 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2
SBT Toán 11 - Chân trời sáng tạo
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Chương 8. Quan hệ vuông góc trong không gian
Bài 4. Khoảng cách trong không gian

Giải bài 4 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 4 trang 68 SBT Toán 11 - Chân trời sáng tạo tập 2

Bài 4 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với phương pháp giải bài tập hiệu quả, giúp các em học sinh tự tin hơn trong quá trình học tập.

Cho hình tứ diện đều ABCD có cạnh bằng \(\sqrt {11} \). Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Đề bài

Cho hình tứ diện đều ABCD có cạnh bằng \(\sqrt {11} \). Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Phương pháp giải - Xem chi tiếtGiải bài 4 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 1

Sử dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau để tính: Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường thẳng đến mặt phẳng song song với nó và chứa đường thẳng còn lại. 

Lời giải chi tiết

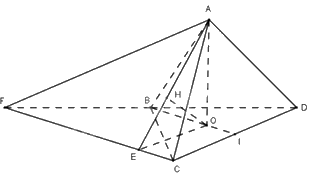
Giải bài 4 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 2

Gọi O là tâm của tam giác đều BCD. Khi đó, \(AO \bot \left( {BCD} \right)\)

Qua C kẻ đường thẳng song song với BI cắt BD tại F. Khi đó, CF//BI nên BI//(ACF)

Suy ra: \(d\left( {AC,BI} \right) = d\left( {BI,\left( {ACF} \right)} \right) = d\left( {O,\left( {ACF} \right)} \right)\)

Ta có: \(BI \bot CD,CF//BI \) \( \Rightarrow CF \bot CD\)

Qua O kẻ đường thẳng song song với CD cắt CF tại E. Ta có: \(OE//CD \) \( \Rightarrow OE\; \bot CF\)

Vì \(OE\; \bot CF,CF \bot AO\left( {do\;AO \bot \left( {BCD} \right)} \right) \) \( \Rightarrow CF \bot \left( {AOE} \right)\)

Trong (AOE), kẻ \(OH \bot AE\left( {H \in AC} \right) \) \( \Rightarrow OH \bot \left( {ACF} \right) \) \( \Rightarrow d\left( {O,\left( {ACF} \right)} \right) = OH\)

Chứng minh được tứ giác OICE là hình chữ nhật. Suy ra \(OE = CI = \frac{{CD}}{2} = \frac{{\sqrt {11} }}{2}\)

Tam giác BCD đều, BI là đường trung tuyến đồng thời là đường cao của tam giác nên \(BI = \frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt {33} }}{2} \) \( \Rightarrow BO = \frac{2}{3}BI = \frac{{\sqrt {33} }}{3}\)

Vì \(AO \bot \left( {BCD} \right) \) \( \Rightarrow AO \bot BO,AO \bot OE\).

Áp dụng định lí Pythagore vào tam giác ABO vuông tại O có: \(AO = \sqrt {A{B^2} - B{O^2}} = \frac{{\sqrt {66} }}{3}\)

Tam giác AOE vuông tại O, đường cao OH có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{E^2}}} = \frac{9}{{66}} + \frac{4}{{11}} = \frac{1}{2}\)

Do đó, \(OH = \sqrt 2 \)

Giải bài 4 trang 68 SBT Toán 11 - Chân trời sáng tạo tập 2: Hướng dẫn chi tiết và dễ hiểu

Bài 4 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về dãy số, cấp số cộng và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế liên quan đến dãy số. Dưới đây là hướng dẫn chi tiết cách giải bài 4 trang 68 SBT Toán 11 Chân trời sáng tạo tập 2:

Đề bài:

Cho dãy số (un) xác định bởi u1 = 1 và un+1 = 2un + 1 với mọi n ≥ 1. Tính u5.

Lời giải:

Để tính u5, ta cần tính lần lượt các số hạng u2, u3, u4, u5 theo công thức đệ quy đã cho:

  • u2 = 2u1 + 1 = 2(1) + 1 = 3
  • u3 = 2u2 + 1 = 2(3) + 1 = 7
  • u4 = 2u3 + 1 = 2(7) + 1 = 15
  • u5 = 2u4 + 1 = 2(15) + 1 = 31

Vậy, u5 = 31.

Phân tích và nhận xét:

Bài tập này giúp học sinh hiểu rõ cách sử dụng công thức đệ quy để tính các số hạng của dãy số. Việc tính toán từng bước một cách cẩn thận là rất quan trọng để tránh sai sót. Ngoài ra, có thể nhận thấy rằng các số hạng của dãy số có dạng 2n - 1, với n là vị trí của số hạng trong dãy.

Mở rộng kiến thức:

Dãy số (un) trong bài tập này là một ví dụ về dãy số được định nghĩa bằng công thức đệ quy. Công thức đệ quy cho phép ta xác định một số hạng của dãy số dựa trên các số hạng trước đó. Ngoài công thức đệ quy, dãy số còn có thể được định nghĩa bằng công thức tổng quát, cho phép ta tính trực tiếp số hạng thứ n của dãy số mà không cần phải tính các số hạng trước đó.

Bài tập tương tự:

Để củng cố kiến thức về dãy số và công thức đệ quy, các em có thể tự giải các bài tập tương tự sau:

  1. Cho dãy số (vn) xác định bởi v1 = 2 và vn+1 = 3vn - 1 với mọi n ≥ 1. Tính v4.
  2. Cho dãy số (wn) xác định bởi w1 = 1 và wn+1 = wn + n với mọi n ≥ 1. Tính w6.

Kết luận:

Giải bài 4 trang 68 SBT Toán 11 Chân trời sáng tạo tập 2 là một bài tập cơ bản nhưng quan trọng trong chương trình học về dãy số. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học sinh tự tin hơn trong quá trình học tập và làm bài kiểm tra.

tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải bài tập Toán 11 và các môn học khác.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN