Giải bài 3 trang 128 SBT Toán 11 Chân trời sáng tạo tập 1

Giải bài 3 trang 128 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 3 trang 128 sách bài tập Toán 11 Chân trời sáng tạo tập 1

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài 3 trang 128, đồng thời cung cấp các kiến thức nền tảng cần thiết.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin hơn trong quá trình học tập môn Toán.

Cho hình hộp ABCD.A’B’C’D’. Chứng minh: a) (BDA’)//(B’D’C). b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C. c) G và G’ chia AC’ thành ba phần bằng nhau.

Đề bài

Cho hình hộp ABCD.A’B’C’D’. Chứng minh:

a) (BDA’)//(B’D’C).

b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C.

c) G và G’ chia AC’ thành ba phần bằng nhau.

Phương pháp giải - Xem chi tiết Giải bài 3 trang 128 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

Lời giải chi tiết

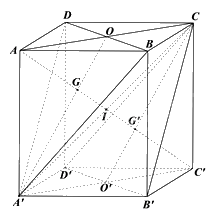
Giải bài 3 trang 128 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

a) Ta có: DD’//BB’ và \(DD' = BB'\) (do ABCD.A’B’C’D’ là hình hộp), suy ra DD’B’B là hình bình hành, suy ra BD//B’D’, mà \(B'D' \subset \left( {B'D'C} \right)\), BD không nằm trong mặt phẳng (B’D’C) nên BD//(B’D’C).

Chứng minh tương tự ta có: DA’//(B’D’C)

Mà BD và DA’ cắt nhau tại D và nằm trong mặt phẳng (BDA’) nên (BDA’)//(B’D’C).

b) Gọi O, O’ lần lượt là tâm của hai đáy ABCD và A’B’C’D’.

Trong hình bình hành AA’C’C gọi I là giao điểm của AC’ và A’C, AC’ cắt A’O tại \({G_1}\)

Trong tam giác AA’C, ta có \({G_1}\) là giao điểm của hai trung tuyến AI và A’O nên \({G_1}\) là trọng tâm của tam giác AA’C. Suy ra \(A'{G_1} = \frac{2}{3}A'O\)

Mà G là trọng tâm của tam giác A’BD nên \(A'G = \frac{2}{3}A'O\)

Do đó, \(G \equiv {G_1}\) hay G là giao điểm của AC’ và A’O.

Chứng minh tương tự ta có trọng tâm G’ của tam giác B’D’C là giao điểm của AC’ và CO’.

Vậy AC’ đi qua trọng tâm của hai tam giác BDA’ và B’D’C.

c) Ta có: \(AG = \frac{2}{3}AI = \frac{2}{3}.\frac{1}{2}AC' = \frac{1}{3}AC',C'G' = \frac{2}{3}C'I = \frac{2}{3}.\frac{1}{2}AC' = \frac{1}{3}AC'\)

Do đó \(GG' = AC' - AG - C'G' = AC' - \frac{1}{3}AC' - \frac{1}{3}AC' = \frac{1}{3}AC'\)

Do đó, \(AG = GG' = G'C'\). Vậy G và G’ chia AC’ thành ba phần bằng nhau.

Giải bài 3 trang 128 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải

Bài 3 trang 128 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về Đạo hàm của hàm số. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm cơ bản, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số, cũng như đạo hàm của hàm hợp. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

Các quy tắc tính đạo hàm: Đạo hàm của hàm số lũy thừa, đạo hàm của hàm số lượng giác, đạo hàm của hàm số mũ, logarit.
Quy tắc đạo hàm của tổng, hiệu, tích, thương: Nắm vững công thức và biết cách áp dụng vào các bài toán cụ thể.
Quy tắc đạo hàm của hàm hợp: Đây là quy tắc quan trọng nhất để giải quyết bài tập này.

Lời giải chi tiết bài 3 trang 128 SBT Toán 11 Chân trời sáng tạo tập 1

Để cung cấp lời giải chính xác, chúng ta cần biết nội dung cụ thể của bài tập. Tuy nhiên, dưới đây là một ví dụ minh họa về cách giải một bài tập tương tự:

Ví dụ: Tính đạo hàm của hàm số f(x) = (x² + 1) * sin(x)

Giải:

Áp dụng quy tắc đạo hàm của tích: (u * v)' = u' * v + u * v'
Đặt u = x² + 1 và v = sin(x)
Tính đạo hàm của u và v: u' = 2x và v' = cos(x)
Thay vào công thức: f'(x) = 2x * sin(x) + (x² + 1) * cos(x)

Các dạng bài tập thường gặp trong bài 3 trang 128

Ngoài việc tính đạo hàm trực tiếp, bài 3 trang 128 còn có thể xuất hiện các dạng bài tập sau:

Tìm đạo hàm cấp hai: Tính đạo hàm của đạo hàm đã tìm được.
Tìm đạo hàm tại một điểm: Thay giá trị x cụ thể vào đạo hàm để tìm giá trị đạo hàm tại điểm đó.
Ứng dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.

Mẹo giải bài tập đạo hàm hiệu quả

Để giải các bài tập về đạo hàm một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:

Nắm vững các công thức đạo hàm cơ bản: Điều này giúp bạn tiết kiệm thời gian và tránh sai sót.
Phân tích cấu trúc của hàm số: Xác định hàm số có dạng nào (tổng, hiệu, tích, thương, hàm hợp) để áp dụng quy tắc đạo hàm phù hợp.
Thực hành thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
Sử dụng các công cụ hỗ trợ: Các công cụ tính đạo hàm trực tuyến có thể giúp bạn kiểm tra lại kết quả và hiểu rõ hơn về quá trình giải.

Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục môn Toán

Tusach.vn tự hào là một trong những website cung cấp lời giải bài tập Toán 11 Chân trời sáng tạo tập 1 uy tín và chất lượng. Chúng tôi cam kết mang đến cho bạn những lời giải chi tiết, dễ hiểu và chính xác nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

Nếu bạn có bất kỳ câu hỏi nào hoặc cần hỗ trợ thêm, đừng ngần ngại liên hệ với chúng tôi. Chúc bạn học tập tốt!