Giải bài 1 trang 117 SBT Toán 11 - Chân trời sáng tạo tập 1

Giải bài 1 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 1 trang 117 sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1.

Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng và kiến thức đã học.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác và dễ hiểu nhất.

Cho hình chóp S. ABCD có đáy ABCD là hình thang, đáy lớn AD. Gọi I và J lần lượt trọng tâm của tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q. a) Chứng minh MN song song với PQ. b) Gọi E là giao điểm của AM và BP, F là giao điểm của CQ và DN. Chứng minh EF song song với MN và PQ.

Đề bài

a) Chứng minh MN song song với PQ.

b) Gọi E là giao điểm của AM và BP, F là giao điểm của CQ và DN. Chứng minh EF song song với MN và PQ.

Phương pháp giải - Xem chi tiết Giải bài 1 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh:

+ Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

+ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Lời giải chi tiết

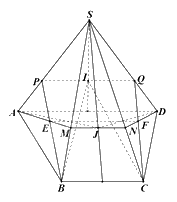
Giải bài 1 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

a) Ta có: AD//BC (do ABCD là hình thang đáy lớn AD).

Mà \(AD \subset \left( {ADJ} \right),BC \subset \left( {SBC} \right),\left( {ADJ} \right) \cap \left( {SBC} \right) = MN\)

Do đó, MN//AD//BC

Chứng minh tương tự ta có: PQ//AD//BC

Suy ra: MN//PQ

b) Ta có: AD//BC (do ABCD là hình thang đáy lớn AD).

Mà \(AD \subset \left( {ADJ} \right),BC \subset \left( {IBC} \right),\left( {ADJ} \right) \cap \left( {IBC} \right) = EF\) nên EF//AD//BC

Mà MN//PQ// AD//BC (theo câu a)

Do đó, MN//EF//QP

Giải bài 1 trang 117 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan và hướng dẫn chi tiết

Bài 1 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng, giúp học sinh củng cố kiến thức về các khái niệm và định lý đã học trong chương trình. Bài tập này thường yêu cầu học sinh vận dụng kiến thức vào giải quyết các bài toán thực tế, đòi hỏi sự hiểu biết sâu sắc và khả năng tư duy logic.

Nội dung bài tập 1 trang 117 SBT Toán 11 Chân trời sáng tạo tập 1

Bài tập 1 thường xoay quanh các chủ đề sau:

Đạo hàm của hàm số: Tính đạo hàm của các hàm số đơn giản, hàm hợp, hàm lượng giác.
Ứng dụng của đạo hàm: Tìm cực trị của hàm số, khảo sát hàm số.
Giới hạn: Tính giới hạn của hàm số tại một điểm hoặc khi x tiến tới vô cùng.
Các bài toán liên quan đến thực tế: Ứng dụng đạo hàm để giải quyết các bài toán về vận tốc, gia tốc, tối ưu hóa.

Lời giải chi tiết bài 1 trang 117 SBT Toán 11 Chân trời sáng tạo tập 1

Để giúp các em học sinh giải quyết bài tập này một cách hiệu quả, tusach.vn xin cung cấp lời giải chi tiết cho từng câu hỏi:

Câu a: (Ví dụ minh họa)

Đề bài: Tính đạo hàm của hàm số f(x) = x² + 2x - 1.

Lời giải:

f'(x) = 2x + 2

Câu b: (Ví dụ minh họa)

Đề bài: Tìm cực trị của hàm số g(x) = x³ - 3x² + 2.

Lời giải:

g'(x) = 3x² - 6x

Giải phương trình g'(x) = 0, ta được x = 0 hoặc x = 2.

Kiểm tra dấu của g'(x) để xác định cực trị.

Kết luận: Hàm số có cực đại tại x = 0 và cực tiểu tại x = 2.

Mẹo giải bài tập Toán 11 Chân trời sáng tạo tập 1 hiệu quả

Để học tốt môn Toán 11 và giải quyết các bài tập một cách hiệu quả, các em nên:

Nắm vững kiến thức cơ bản: Hiểu rõ các định nghĩa, định lý và công thức đã học.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
Sử dụng tài liệu tham khảo: Tham khảo sách giáo khoa, sách bài tập, các trang web học tập trực tuyến.
Hỏi thầy cô giáo: Nếu gặp khó khăn, hãy hỏi thầy cô giáo để được hướng dẫn và giải đáp.

Tại sao nên chọn tusach.vn để học Toán 11?

tusach.vn là một trang web học tập trực tuyến uy tín, cung cấp:

Lời giải chi tiết và dễ hiểu: Các lời giải được trình bày rõ ràng, logic, giúp các em dễ dàng nắm bắt kiến thức.
Đa dạng tài liệu học tập: Sách giáo khoa, sách bài tập, đề thi, bài giảng,...
Cộng đồng học tập sôi động: Các em có thể trao đổi, học hỏi kinh nghiệm với các bạn học sinh khác.
Hỗ trợ 24/7: Đội ngũ hỗ trợ luôn sẵn sàng giải đáp các thắc mắc của các em.

Chúc các em học tập tốt và đạt kết quả cao trong môn Toán 11!