Giải bài 1 trang 68 SBT Toán 11 Chân trời sáng tạo tập 2

Giải bài 1 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 1 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2

Bài 1 trang 68 SBT Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân.

tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết \(SA = \frac{{a\sqrt 6 }}{2}\).

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 1 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 1

Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)).

Lời giải chi tiết

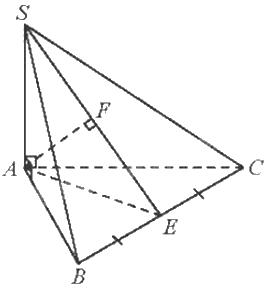
Giải bài 1 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 2

Gọi E là trung điểm của BC. Vì tam giác ABC đều nên AE là đường trung tuyến đồng thời là đường cao. Do đó, \(AE \bot BC\)

Ta có: \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\), mà \(AE \bot BC\). Suy ra: \(BC \bot \left( {SAE} \right)\)

Kẻ \(AF \bot SE\left( {S \in SE} \right)\). Vì \(BC \bot \left( {SAE} \right)\)\( \Rightarrow BC \bot AF\)

Ta có: \(BC \bot AF,AF \bot SE,\) BC và SE cắt nhau tại E và nằm trong mặt phẳng (SBC) nên \(AF \bot \left( {SBC} \right)\). Khi đó, AF là khoảng cách từ A đến mặt phẳng (SBC).

Vì tam giác ABC đều nên \(\widehat {ABC} = {60^0}\).

Tam giác ABE vuông tại E có: \(AE = AB.\sin \widehat {ABC} = \frac{{a\sqrt 3 }}{2}\)

Vì \(SA \bot \left( {ABC} \right),AE \subset \left( {ABC} \right) \Rightarrow SA \bot AE\)

Tam giác AES vuông tại A, có AF là đường cao nên:

\(\frac{1}{{A{F^2}}} = \frac{1}{{A{E^2}}} + \frac{1}{{S{A^2}}} = \frac{4}{{3{a^2}}} + \frac{4}{{6{a^2}}} = \frac{2}{{{a^2}}} \Rightarrow AF = \frac{{a\sqrt 2 }}{2}\)

Giải bài 1 trang 68 SBT Toán 11 Chân trời sáng tạo tập 2: Tổng quan và Phương pháp giải

Bài 1 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất của dãy số để giải quyết các vấn đề thực tế. Để giải bài tập này hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:

Dãy số: Định nghĩa, các loại dãy số (dãy số hữu hạn, dãy số vô hạn, dãy số tăng, dãy số giảm).
Cấp số cộng: Định nghĩa, công thức tính số hạng tổng quát, tổng n số hạng đầu.
Cấp số nhân: Định nghĩa, công thức tính số hạng tổng quát, tổng n số hạng đầu.

Lời giải chi tiết bài 1 trang 68 SBT Toán 11 Chân trời sáng tạo tập 2

Để cung cấp lời giải chính xác, chúng ta cần biết nội dung cụ thể của bài tập. Giả sử bài tập yêu cầu:

“Cho dãy số (u_n) được xác định bởi u₁ = 2 và u_n+1 = 2u_n + 1. Tính u₅.”

Lời giải:

u₁ = 2
u₂ = 2u₁ + 1 = 2(2) + 1 = 5
u₃ = 2u₂ + 1 = 2(5) + 1 = 11
u₄ = 2u₃ + 1 = 2(11) + 1 = 23
u₅ = 2u₄ + 1 = 2(23) + 1 = 47

Vậy u₅ = 47.

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài tập trên, còn rất nhiều dạng bài tập tương tự liên quan đến dãy số, cấp số cộng và cấp số nhân. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:

Tìm số hạng tổng quát của dãy số: Sử dụng công thức đệ quy hoặc công thức tổng quát của cấp số cộng/cấp số nhân.
Tính tổng n số hạng đầu của dãy số: Sử dụng công thức tính tổng của cấp số cộng/cấp số nhân.
Chứng minh một số là số hạng của dãy số: Giải phương trình u_n = a (với a là số cần kiểm tra) để tìm n. Nếu n là số nguyên dương thì a là số hạng của dãy số.

Mẹo giải bài tập dãy số, cấp số cộng và cấp số nhân

Để giải bài tập về dãy số, cấp số cộng và cấp số nhân một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:

Nắm vững các công thức: Công thức tính số hạng tổng quát, tổng n số hạng đầu là những công cụ quan trọng để giải bài tập.
Phân tích kỹ đề bài: Xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
Sử dụng phương pháp quy nạp: Phương pháp này có thể giúp bạn chứng minh các tính chất của dãy số.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn làm quen với các dạng bài và rèn luyện kỹ năng giải toán.

Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín

Tusach.vn là một website cung cấp đầy đủ và chính xác các lời giải bài tập Toán 11, bao gồm cả sách giáo khoa và sách bài tập Chân trời sáng tạo. Chúng tôi luôn cập nhật những nội dung mới nhất và cung cấp các giải pháp học tập hiệu quả cho học sinh. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!