Đề bài
Cho tứ diện ABCD có tam giác BCD vuông cân tại B và \(AB \bot \left( {BCD} \right)\). Cho biết \(BC = a\sqrt 2 ,AB = \frac{a}{{\sqrt 3 }}\). Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
Lời giải chi tiết
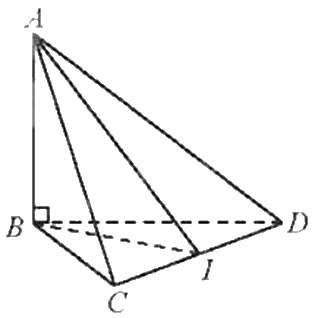
Gọi I là trung điểm của CD.
Tam giác BCD vuông cân tại B nên BI là đường trung tuyến đồng thời là đường cao.
Do đó, \(BI \bot CD\).
Tam giác BCD vuông cân tại B nên \(BC = BD = a\sqrt 2 \)
Vì \(AB \bot \left( {BCD} \right),BD \subset \left( {BCD} \right) \Rightarrow AB \bot BD\). Do đó, tam giác ABD vuông tại B.
Áp dụng định lí Pythagore vào tam giác ABD vuông tại B có:
\(AD = \sqrt {A{B^2} + B{D^2}} = \sqrt {{{\left( {\frac{a}{{\sqrt 3 }}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = \frac{{a\sqrt {21} }}{3}\)
Vì \(AB \bot \left( {BCD} \right),BC \subset \left( {BCD} \right) \Rightarrow AB \bot BC\). Do đó, tam giác ABC vuông tại B.
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {\frac{a}{{\sqrt 3 }}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = \frac{{a\sqrt {21} }}{3}\)
Do đó, \(AC = AD\) nên tam giác ACD cân tại A.
Nên AI là đường trung tuyến đồng thời là đường cao. Suy ra, \(AI \bot CD\).
Ta có: CD là giao tuyến của hai mặt phẳng (BCD) và (ACD)\(BI \bot CD,AI \bot CD,BI \subset \left( {BCD} \right),AI \subset \left( {ACD} \right)\). Nên \(\left( {\left( {ACD} \right),\left( {BCD} \right)} \right) = \left( {AI,BI} \right) = \widehat {AIB}\)
Áp dụng định lí Pythagore vào tam giác BCD vuông tai B có: \(CD = \sqrt {B{C^2} + B{D^2}} = 2a\)
Tam giác BCD vuông cân tại B nên \(BI = \frac{{CD}}{2} = a\)
Vì \(AB \bot \left( {BCD} \right),BI \subset \left( {BCD} \right) \Rightarrow AB \bot BI\). Do đó, tam giác ABI vuông tại B.
Do đó, \(\tan \widehat {AIB} = \frac{{AB}}{{BI}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {AIB} = {30^0}\)
