Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 3 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2
SBT Toán 11 - Chân trời sáng tạo
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Chương 8. Quan hệ vuông góc trong không gian
Bài 5. Góc giữa đường thẳng và mặt phẳng Góc nhị diện

Giải bài 3 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 3 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài 3 trang 73, đồng thời cung cấp kiến thức nền tảng cần thiết để giải quyết các bài toán tương tự.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả và dễ tiếp cận nhất cho học sinh.

Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).

Đề bài

Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).

Phương pháp giải - Xem chi tiếtGiải bài 3 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2 1

+ Sử dụng kiến thức về góc nhị diện: Cho hai nửa mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\) có chung bờ là đường thẳng d. Hình tạo bởi \(\left( {{P_1}} \right)\), \(\left( {{Q_1}} \right)\) và d được gọi là góc nhị diện tạo bởi \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\), kí hiệu \(\left[ {{P_1},d,{Q_1}} \right]\).

+ Sử dụng kiến thức về góc phẳng nhị diện để tính: Góc phẳng nhị diện của góc nhị diện có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.

Lời giải chi tiết

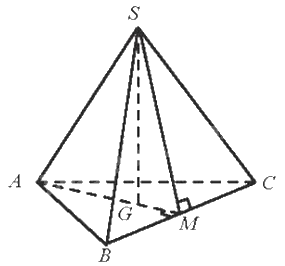
Giải bài 3 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2 2

Gọi M là trung điểm của BC, G là trọng tâm của tam giác ABC.

Suy ra, \(SG \bot \left( {ABC} \right),SM \bot BC,AM \bot BC\)

Do đó, góc SMG là góc phẳng nhị diện \(\left[ {S,BC,A} \right]\)

Vì tam giác ABC đều cạnh a nên \(\widehat {ABC} \) \( = {60^0},AB \) \( = a\), AM là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABM vuông tại M. Suy ra: \(AM \) \( = AB.\sin {60^0} \) \( = \frac{{a\sqrt 3 }}{2}\)

Vì G là trọng tâm tam giác ABC nên \(GM \) \( = \frac{1}{3}AM \) \( = \frac{{a\sqrt 3 }}{6}\)

Vì tam giác SBC đều nên SM là đường trung tuyến đồng thời là đường cao.

Áp dụng định lí Pythagore vào tam giác SBM vuông tại G ta có:

\(SM \) \( = \sqrt {S{B^2} - B{M^2}} \) \( = \frac{{a\sqrt 6 }}{6}\)

Vì \(SG \bot \left( {ABC} \right) \) \( \Rightarrow SG \bot GM\). Áp dụng định lí Pythagore vào tam giác SGM vuông tại G ta có: \(SG \) \( = \sqrt {S{M^2} - G{M^2}} \) \( = \frac{{a\sqrt 3 }}{6}\)

Vì \(GM \) \( = SG\left( { = \frac{{a\sqrt 3 }}{6}} \right),\widehat {SGM} \) \( = {90^0}\) nên tam giác SMG vuông cân tại G.

Do đó, \(\widehat {SMG} \) \( = {45^0}\)

Giải bài 3 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2: Tổng quan và Phương pháp giải

Bài 3 trang 73 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về Đạo hàm của hàm số. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm cơ bản, bao gồm đạo hàm của hàm số đơn thức, đa thức, và các hàm số hợp. Việc nắm vững các quy tắc này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.

Nội dung bài tập 3 trang 73

Bài 3 thường yêu cầu học sinh:

  • Tính đạo hàm của các hàm số cho trước.
  • Tìm đạo hàm cấp hai của hàm số.
  • Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.

Lời giải chi tiết bài 3 trang 73

Để giải bài 3 trang 73 một cách hiệu quả, bạn cần thực hiện theo các bước sau:

  1. Xác định hàm số cần tính đạo hàm.
  2. Áp dụng các quy tắc tính đạo hàm phù hợp. Ví dụ:
    • Đạo hàm của hàm số lũy thừa: (xn)' = nxn-1
    • Đạo hàm của hàm số đa thức: (u + v)' = u' + v'
    • Đạo hàm của hàm số hợp: (f(g(x)))' = f'(g(x)) * g'(x)
  3. Thực hiện các phép tính toán một cách cẩn thận.
  4. Kiểm tra lại kết quả.

Ví dụ minh họa

Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1. Ta thực hiện như sau:

f'(x) = (3x2)' + (2x)' + (-1)'

f'(x) = 6x + 2 + 0

f'(x) = 6x + 2

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài 3 trang 73, bạn có thể gặp các bài tập tương tự với các hàm số phức tạp hơn. Để giải quyết các bài tập này, bạn cần:

  • Nắm vững các quy tắc tính đạo hàm nâng cao, như đạo hàm của hàm số lượng giác, hàm số mũ, hàm số logarit.
  • Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
  • Sử dụng các công cụ hỗ trợ tính đạo hàm trực tuyến để kiểm tra kết quả.

Tài liệu tham khảo hữu ích

Để học tập hiệu quả hơn, bạn có thể tham khảo các tài liệu sau:

  • Sách giáo khoa Toán 11 Chân trời sáng tạo tập 2
  • Sách bài tập Toán 11 Chân trời sáng tạo tập 2
  • Các trang web học toán trực tuyến uy tín

Kết luận

Bài 3 trang 73 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn khi giải quyết các bài toán tương tự. Chúc bạn học tập tốt!

Quy tắcVí dụ
Đạo hàm của hàm số lũy thừa(x3)' = 3x2
Đạo hàm của hàm số đa thức(2x2 + 5x - 3)' = 4x + 5

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN