Giải bài 12 trang 95 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 12 trang 95 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Tusach.vn xin giới thiệu lời giải chi tiết bài 12 trang 95 SBT Toán 11 Chân trời sáng tạo tập 1. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo tập 1.
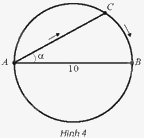
Tại một bể bơi có dạng hình tròn có đường kính \(AB = 10m\), một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi \(S\left( \alpha \right)\) là quãng đường người đó đã di chuyển. a) Viết công thức tính \(S\left( \alpha \right)\) theo \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\). b) Xét tính liên tục của hàm số \(y = S\left( \alpha \right)\)
Đề bài
Tại một bể bơi có dạng hình tròn có đường kính \(AB = 10m\), một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi \(S\left( \alpha \right)\) là quãng đường người đó đã di chuyển.
a) Viết công thức tính \(S\left( \alpha \right)\) theo \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\).
b) Xét tính liên tục của hàm số \(y = S\left( \alpha \right)\) trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\).
c) Tính các giới hạn \(\mathop {\lim }\limits_{\alpha \to {0^ + }} S\left( \alpha \right)\) và \(\mathop {\lim }\limits_{\alpha \to {{\frac{\pi }{2}}^ + }} S\left( \alpha \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các phép toán về giới hạn hữu hạn của hàm số để tính: Cho \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L,\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = M\): \(\mathop {\lim }\limits_{x \to x_0^ + } \left[ {f\left( x \right) \pm g\left( x \right)} \right] = L \pm M\).
Lời giải chi tiết
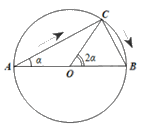
a) Kí hiệu O là tâm hình tròn.
Do tam giác ABC vuông tại C nên \(AC = AB\cos \alpha = 10\cos \alpha \left( m \right)\)
Ta có: \(\widehat {BOC} = 2\widehat {BAC} = 2\alpha \) nên độ dài cung BC là: \(l = OB.\widehat {BOC} = 5.2\alpha = 10\alpha \left( m \right)\)
Quãng đường di chuyển của người đó là:
\(S\left( \alpha \right) = AC + l = 10\cos \alpha + 10\alpha = 10\left( {\cos \alpha + \alpha } \right)\)(m) \(\left( {0 < \alpha < \frac{\pi }{2}} \right)\)
b) Do các hàm số \(y = \alpha ,y = \cos \alpha \) liên tục trên \(\mathbb{R}\) nên hàm số \(y = S\left( \alpha \right)\) liên tục trên \(\left( {0;\frac{\pi }{2}} \right)\).
c) \(\mathop {\lim }\limits_{\alpha \to {0^ + }} S\left( \alpha \right) = \mathop {\lim }\limits_{\alpha \to {0^ + }} 10\left( {\alpha + \cos \alpha } \right) = 10\left( {\mathop {\lim }\limits_{\alpha \to {0^ + }} \alpha + \mathop {\lim }\limits_{x \to {0^ + }} \cos \alpha } \right) = 10\left( {0 + 1} \right) = 10\)
\(\mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} S\left( \alpha \right) = \mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} 10\left( {\alpha + \cos \alpha } \right) = 10\left( {\mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} \alpha + \mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} \cos \alpha } \right) = 10\left( {\frac{\pi }{2} + 0} \right) = 5\pi \)
Giải bài 12 trang 95 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải
Bài 12 trang 95 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh xác định các yếu tố của phép biến hình affine, tìm ảnh của một điểm hoặc một đường thẳng qua phép biến hình đó, hoặc chứng minh một tính chất liên quan đến phép biến hình affine.
Nội dung bài tập 12 trang 95 SBT Toán 11 Chân trời sáng tạo tập 1
Bài tập 12 thường bao gồm các dạng bài sau:
- Dạng 1: Xác định phép biến hình affine dựa trên các thông tin cho trước.
- Dạng 2: Tìm ảnh của một điểm hoặc một đường thẳng qua phép biến hình affine.
- Dạng 3: Chứng minh một tính chất liên quan đến phép biến hình affine.
- Dạng 4: Ứng dụng phép biến hình affine vào giải quyết các bài toán hình học.
Phương pháp giải bài tập 12 trang 95 SBT Toán 11 Chân trời sáng tạo tập 1
Để giải quyết bài tập 12 trang 95 SBT Toán 11 Chân trời sáng tạo tập 1 hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Khái niệm về phép biến hình affine: Hiểu rõ định nghĩa, tính chất và các yếu tố của phép biến hình affine.
- Ma trận của phép biến hình affine: Biết cách biểu diễn một phép biến hình affine bằng ma trận.
- Các phép biến hình affine cơ bản: Nắm vững các phép biến hình affine cơ bản như phép tịnh tiến, phép quay, phép co giãn và phép chiếu.
- Ứng dụng của phép biến hình affine: Biết cách ứng dụng phép biến hình affine vào giải quyết các bài toán hình học.
Lời giải chi tiết bài 12 trang 95 SBT Toán 11 Chân trời sáng tạo tập 1
Bài 12: (Giả sử đây là nội dung bài tập cụ thể, cần thay thế bằng nội dung thật) Cho điểm A(1; 2) và đường thẳng d: x + y - 3 = 0. Tìm ảnh của điểm A và đường thẳng d qua phép biến hình affine f được xác định bởi:
f(x; y) = (x + 2y - 1; 3x - y + 2)
Giải:
- Tìm ảnh của điểm A:
f(1; 2) = (1 + 2*2 - 1; 3*1 - 2 + 2) = (4; 3)
Vậy ảnh của điểm A là A'(4; 3).
- Tìm ảnh của đường thẳng d:
Đặt x' = x + 2y - 1 và y' = 3x - y + 2. Giải hệ phương trình này để tìm x và y theo x' và y'.
Từ x' = x + 2y - 1 => x = x' - 2y + 1
Thay vào y' = 3x - y + 2, ta được: y' = 3(x' - 2y + 1) - y + 2 = 3x' - 6y + 3 - y + 2 = 3x' - 7y + 5
=> 7y = 3x' - y' + 5 => y = (3x' - y' + 5)/7
Thay y vào x = x' - 2y + 1, ta được: x = x' - 2((3x' - y' + 5)/7) + 1 = x' - (6x' - 2y' + 10)/7 + 1 = (7x' - 6x' + 2y' - 10 + 7)/7 = (x' + 2y' - 3)/7
Thay x và y vào phương trình đường thẳng d: x + y - 3 = 0, ta được:
(x' + 2y' - 3)/7 + (3x' - y' + 5)/7 - 3 = 0
=> x' + 2y' - 3 + 3x' - y' + 5 - 21 = 0
=> 4x' + y' - 19 = 0
Vậy ảnh của đường thẳng d là d': 4x + y - 19 = 0.
Lưu ý khi giải bài tập về phép biến hình affine
- Luôn kiểm tra lại các bước tính toán để tránh sai sót.
- Sử dụng các công thức và định lý liên quan đến phép biến hình affine một cách chính xác.
- Rèn luyện kỹ năng giải toán thường xuyên để nắm vững kiến thức và phương pháp giải.
Hy vọng với lời giải chi tiết và phương pháp giải trên, các bạn học sinh có thể tự tin giải quyết bài tập 12 trang 95 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1. Chúc các bạn học tốt!