Giải bài 4 trang 51 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Tổng quan nội dung
Giải bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2
Bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính các góc giữa các đường thẳng sau:
Đề bài
Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính các góc giữa các đường thẳng sau:
a) IJ và DC;
b) MN và IJ.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai đường thẳng trong không gian để tính: Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b.
Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\).
Lời giải chi tiết
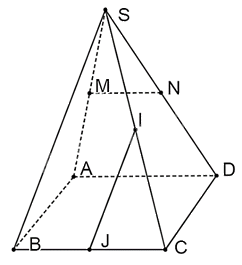
a) Vì I, J lần lượt là trung điểm của SC, BC nên IJ là đường trung bình của tam giác SBC. Do đó, IJ//SB.
Vì tứ giác ABCD có tất cả các cạnh bằng a nên tứ giác ABCD là hình thoi. Do đó, DC//AB.
Do đó, \(\left( {IJ,CD} \right) = \left( {SB,AB} \right) = \widehat {SBA}\)
Tam giác SBA có ba cạnh bằng a nên tam giác SBA là tam giác đều. Suy ra, \(\widehat {SBA} = {60^0}\)
b) Vì M, N lần lượt là trung điểm của SA, SD nên MN là đường trung bình của tam giác SAD. Do đó, MN//AD.
Vì tứ giác ABCD là hình thoi nên AD//BC nên MN//BC.
Do đó, \(\left( {MN,IJ} \right) = \left( {BC,SB} \right) = \widehat {SBC}\)
Tam giác SBC có ba cạnh bằng a nên tam giác SBC đều. Suy ra \(\widehat {SBC} = {60^0}\)
Giải bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2: Tổng quan và Phương pháp
Bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh:
- Tính đạo hàm của hàm số tại một điểm.
- Tìm đạo hàm của hàm số.
- Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến, khoảng đơn điệu, cực trị,...
Để giải bài tập này hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
- Định nghĩa đạo hàm.
- Các quy tắc tính đạo hàm (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...).
- Đạo hàm của các hàm số cơ bản (hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit,...).
Lời giải chi tiết bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2
Dưới đây là lời giải chi tiết bài 4 trang 51 SBT Toán 11 Chân trời sáng tạo tập 2. (Lưu ý: Nội dung bài tập cụ thể sẽ được trình bày chi tiết tại đây, giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x^3 - 2x + 1 tại x = 2)
Ví dụ minh họa:
Cho hàm số f(x) = x3 - 2x + 1. Tính f'(2).
- Bước 1: Tính đạo hàm f'(x)
- Bước 2: Thay x = 2 vào f'(x)
- Kết luận: f'(2) = 10
f'(x) = 3x2 - 2
f'(2) = 3(2)2 - 2 = 12 - 2 = 10
Mở rộng và Bài tập tương tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự với các hàm số khác nhau. Ví dụ:
- Tính đạo hàm của hàm số g(x) = 2x2 + 5x - 3 tại x = 1.
- Tìm đạo hàm của hàm số h(x) = sin(x) + cos(x).
Lưu ý khi giải bài tập về đạo hàm
Khi giải bài tập về đạo hàm, các em cần chú ý:
- Nắm vững các quy tắc tính đạo hàm.
- Kiểm tra lại kết quả sau khi tính toán.
- Vận dụng đạo hàm để giải quyết các bài toán thực tế một cách linh hoạt.
Tusach.vn - Đồng hành cùng học sinh
tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 2. Hãy truy cập tusach.vn để học Toán 11 hiệu quả hơn!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
| Bảng đạo hàm một số hàm số cơ bản | |