Giải bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài 12 trang 85, đồng thời cung cấp kiến thức nền tảng cần thiết để giải quyết các bài toán tương tự.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả và dễ dàng tiếp cận nhất cho học sinh.
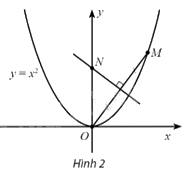
Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {t,{t^2}} \right),t > 0\), nằm trên đường parabol \(y = {x^2}\). Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi M dần đến điểm O?
Giải bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải
Bài 12 trang 85 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về Đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về định nghĩa đạo hàm, các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương, hàm hợp) và đạo hàm của một số hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit) để giải quyết các bài toán cụ thể.
Nội dung bài tập 12 trang 85 SBT Toán 11 Chân trời sáng tạo tập 1
Thông thường, bài tập 12 trang 85 sẽ bao gồm các dạng bài sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước tại một điểm hoặc trên một khoảng xác định.
- Tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm cấp hai của một hàm số.
- Ứng dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến: Tìm phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho trước.
- Ứng dụng đạo hàm để xét tính đơn điệu của hàm số: Xác định khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Để giải bài 12 trang 85 một cách hiệu quả, bạn cần:
- Nắm vững định nghĩa đạo hàm: Đạo hàm của hàm số f(x) tại điểm x0 được định nghĩa là giới hạn của tỷ số \frac{f(x) - f(x_0)}{x - x_0} khi x tiến tới x0.
- Thành thạo các quy tắc tính đạo hàm: Sử dụng các quy tắc tính đạo hàm để đơn giản hóa việc tính đạo hàm của các hàm số phức tạp.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
Dưới đây là ví dụ về cách giải một dạng bài tập thường gặp trong bài 12 trang 85:
Ví dụ: Tính đạo hàm của hàm số f(x) = x^3 + 2x^2 - 5x + 1
Giải:
Áp dụng quy tắc đạo hàm của tổng, hiệu và lũy thừa, ta có:
f'(x) = 3x^2 + 4x - 5
Mẹo giải nhanh và hiệu quả
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả bằng cách sử dụng các quy tắc đạo hàm đã học.
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính đạo hàm của một số hàm số phức tạp một cách nhanh chóng và chính xác.
- Tham khảo các nguồn tài liệu khác: Nếu bạn gặp khó khăn trong việc giải bài tập, hãy tham khảo các nguồn tài liệu khác như sách giáo khoa, sách tham khảo, hoặc các trang web học tập trực tuyến.
Tài liệu tham khảo hữu ích
Để học tốt môn Toán 11 và giải quyết các bài tập trong sách bài tập, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 - Chân trời sáng tạo
- Sách bài tập Toán 11 - Chân trời sáng tạo
- Các trang web học tập trực tuyến như tusach.vn, loigiaihay.com, vted.vn
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 một cách hiệu quả. Chúc bạn học tập tốt!
