Giải bài 6 trang 134 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 6 trang 134 SBT Toán 11 Chân trời sáng tạo tập 1
Bài 6 trang 134 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S. ABCD, đáy ABCD là hình thang có đáy lớn AB và \(AD = a\). Mặt bên SAB là tam giác cân tại S, \(SA = a\); mặt phẳng (R) song song với (SAB) và cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q. a) Chứng minh MNPQ là hình thang cân. b) Đặt \(x = AM\) với \(0 < x < a\). Tính MQ theo a và x.
Đề bài
Cho hình chóp S. ABCD, đáy ABCD là hình thang có đáy lớn AB và \(AD = a\). Mặt bên SAB là tam giác cân tại S, \(SA = a\); mặt phẳng (R) song song với (SAB) và cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q.
a) Chứng minh MNPQ là hình thang cân.
b) Đặt \(x = AM\) với \(0 < x < a\). Tính MQ theo a và x.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất của hai mặt phẳng song song để chứng minh: Cho hai mặt phẳng (P) và (Q) song song với nhau. Nếu mặt phẳng (R) cắt (P) thì cắt (Q) và hai giao tuyến của chúng song song với nhau.
Lời giải chi tiết
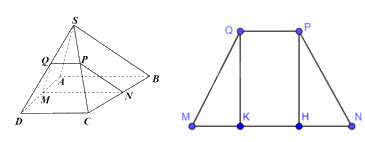
Ta có: Giao tuyến của mặt phẳng (ABCD) và (R) là MN, giao tuyến của mặt phẳng (ABCD) và (SAB) là AB. Mà (R)//(SAB) nên MN//AB.
Chứng minh tương tự ta có: các mặt phẳng (SAD), (SCB), (SCD) cắt hai mặt phẳng song song (R) và (SAB) theo các cặp giao tuyến song song.
Suy ra: MQ//SA, NP//SB, QP//CD//AB.
Do đó, MN//PQ nên tứ giác MNPQ là hình thang.
Ta có: \(\frac{{MQ}}{{SA}} = \frac{{DM}}{{DA}} = \frac{{CN}}{{CB}} = \frac{{NP}}{{SB}}\) (hệ quả định lí Thalès) và \(SA = SB \Rightarrow MQ = NP\)
Kẻ QK vuông góc với MN tại K, PH vuông góc với MN tại H.
Chứng minh được \(\Delta MKQ = \Delta NHP\left( {ch - cgv} \right) \Rightarrow \widehat {QMK} = \widehat {PNH}\)
Do đó, hình thang MNPQ là hình thang cân.
b) Ta có: \(\frac{{MQ}}{{SA}} = \frac{{DM}}{{DA}} \Rightarrow \frac{{MQ}}{a} = \frac{{a - x}}{a} \Rightarrow MQ = a - x\)
Giải bài 6 trang 134 SBT Toán 11 Chân trời sáng tạo tập 1: Hướng dẫn chi tiết và đáp án
Bài 6 trang 134 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm cực trị của hàm số, một kỹ năng quan trọng trong toán học và có ứng dụng thực tế cao.
Đề bài bài 6 trang 134 SBT Toán 11 Chân trời sáng tạo tập 1
(Nội dung đề bài sẽ được chèn vào đây. Ví dụ:) Tìm cực trị của các hàm số sau:
- a) y = x3 - 3x2 + 2
- b) y = -x4 + 4x2 - 1
Phương pháp giải bài tập cực trị hàm số
Để giải bài tập tìm cực trị của hàm số, chúng ta cần thực hiện các bước sau:
- Tính đạo hàm cấp một (y') của hàm số.
- Tìm các điểm dừng của hàm số bằng cách giải phương trình y' = 0.
- Lập bảng xét dấu đạo hàm cấp một (y') để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kết luận về cực trị: Nếu y' đổi dấu từ dương sang âm tại một điểm thì điểm đó là điểm cực đại. Nếu y' đổi dấu từ âm sang dương tại một điểm thì điểm đó là điểm cực tiểu.
Giải chi tiết bài 6 trang 134 SBT Toán 11 Chân trời sáng tạo tập 1
a) y = x3 - 3x2 + 2
- Tính đạo hàm cấp một: y' = 3x2 - 6x
- Tìm điểm dừng: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
- Lập bảng xét dấu y':
x -∞ 0 2 +∞ y' + - + - Kết luận:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là y(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y(2) = -2.
b) y = -x4 + 4x2 - 1
(Giải tương tự như phần a, trình bày chi tiết các bước)
Lưu ý khi giải bài tập cực trị hàm số
- Luôn kiểm tra điều kiện xác định của hàm số.
- Chú ý đến các điểm không xác định của đạo hàm.
- Sử dụng đạo hàm cấp hai để xác định bản chất của điểm dừng (cực đại, cực tiểu) nếu cần thiết.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài 6 trang 134 SBT Toán 11 Chân trời sáng tạo tập 1 và các bài tập tương tự. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ!