Giải bài 2 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2

Giải bài 2 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 2 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác nhất cho bài tập 2 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.

Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết bài toán này một cách hiệu quả.

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.

Đề bài

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.

a) Tính khoảng cách từ S đến mặt phẳng (ABC).

b) Tính khoảng cách từ M đến mặt phẳng (SAG).

Phương pháp giải - Xem chi tiết Giải bài 2 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 1

Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)).

Lời giải chi tiết

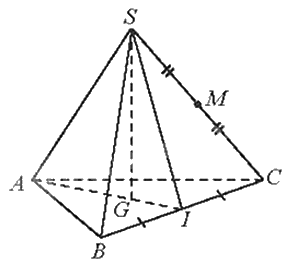
Giải bài 2 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 2

a) Vì S.ABC là hình chóp tam giác đều, G là trọng tâm của tam giác ABC nên \(SG \bot \left( {ABC} \right)\). Do đó, \(d\left( {S;\left( {ABC} \right)} \right) = SG\)

Vì tam giác ABC đều nên \(\widehat {ABC} = {60^0}\).

Gọi I là giao điểm của AG và BC. Khi đó, \(AG = \frac{2}{3}AI\)

Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABI vuông tại I. Suy ra: \(AI = AB.\sin \widehat {ABC} = \frac{{3a\sqrt 3 }}{2} \Rightarrow AG = a\sqrt 3 \)

Vì \(SG \bot \left( {ABC} \right),AG \subset \left( {ABC} \right) \Rightarrow SG \bot AG\)

Áp dụng định lí Pythagore vào tam giác ASG vuông tại G có:

\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {a\sqrt 3 } \right)}^2}} = a\)

b) Vì \(SC \cap \left( {SAG} \right) = S \) \(\Rightarrow \frac{{d\left( {M,\left( {SAG} \right)} \right)}}{{d\left( {C,\left( {SAG} \right)} \right)}} = \frac{{MS}}{{CS}} = \frac{1}{2} \) \(\Rightarrow d\left( {M,\left( {SAG} \right)} \right) = \frac{1}{2}d\left( {C,\left( {SAG} \right)} \right)\)

Vì \(CB \bot AI,CB \bot SG \Rightarrow CB \bot \left( {SAG} \right)\). Mà \(CB \cap \left( {SAG} \right) = I\)

Do đó, \(d\left( {C,\left( {SAG} \right)} \right) = CI = \frac{1}{2}BC = \frac{{3a}}{2}\). Vậy \(d\left( {M,\left( {SAG} \right)} \right) = \frac{{3a}}{4}\)

Giải bài 2 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2: Tổng quan

Bài 2 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về định nghĩa đạo hàm, các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và đạo hàm hàm hợp để giải quyết các bài toán cụ thể.

Nội dung bài tập 2 trang 68

Bài tập 2 thường bao gồm các dạng bài sau:

Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước tại một điểm hoặc trên một khoảng xác định.
Tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm cấp hai của một hàm số.
Ứng dụng đạo hàm để giải quyết các bài toán thực tế: Ví dụ như tìm vận tốc, gia tốc của một vật chuyển động.

Lời giải chi tiết bài 2 trang 68

Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lời giải sẽ bao gồm các bước thực hiện, giải thích rõ ràng và các lưu ý quan trọng.

Ví dụ minh họa (Giả định một phần của bài tập):

Câu a: Tính đạo hàm của hàm số f(x) = x² + 3x - 2

Lời giải:

Áp dụng quy tắc đạo hàm của tổng: f'(x) = (x²)' + (3x)' - (2)'
Áp dụng quy tắc đạo hàm của lũy thừa: (x²)' = 2x
Áp dụng quy tắc đạo hàm của hằng số: (2)' = 0
Áp dụng quy tắc đạo hàm của tích: (3x)' = 3
Vậy, f'(x) = 2x + 3

Mẹo giải bài tập đạo hàm hiệu quả

Nắm vững định nghĩa đạo hàm: Hiểu rõ ý nghĩa của đạo hàm và cách tính đạo hàm theo định nghĩa.
Học thuộc các quy tắc tính đạo hàm: Các quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp là những công cụ quan trọng để giải quyết các bài toán đạo hàm.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
Sử dụng các công cụ hỗ trợ: Các công cụ tính đạo hàm trực tuyến có thể giúp bạn kiểm tra lại kết quả và hiểu rõ hơn về quá trình tính đạo hàm.

Tài liệu tham khảo hữu ích

Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:

Các trang web học toán trực tuyến: Ví dụ như Khan Academy, VietJack,...
Các video hướng dẫn giải toán: Tìm kiếm trên YouTube với các từ khóa như "giải bài tập đạo hàm lớp 11".
Các diễn đàn học tập: Tham gia các diễn đàn để trao đổi kiến thức và kinh nghiệm với các bạn học sinh khác.

Kết luận

Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết bài tập 2 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 một cách hiệu quả. Chúc bạn học tập tốt!

Giải bài 2 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 2 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2

Giải bài 2 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2: Tổng quan

Nội dung bài tập 2 trang 68

Lời giải chi tiết bài 2 trang 68

Ví dụ minh họa (Giả định một phần của bài tập):

Mẹo giải bài tập đạo hàm hiệu quả

Tài liệu tham khảo hữu ích

Kết luận

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN