Giải bài 2 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 2 trang 161 sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho học sinh. Hãy cùng Tusach.vn khám phá lời giải bài 2 này ngay nhé!
Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần. Kết quả được tổng hợp lại ở bảng sau: a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên. b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa nhất. Cô nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa?
Đề bài
Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần. Kết quả được tổng hợp lại ở bảng sau:

a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên.
b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa nhất. Cô nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa?
Phương pháp giải - Xem chi tiết
a) + Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
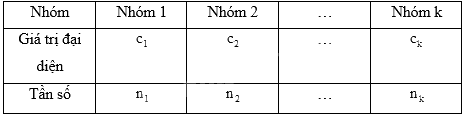
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
b) Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết
a) Ta hiệu chỉnh lại bảng số liệu bao gồm giá trị đại diện:

Cỡ mẫu \(n = 44\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{7.8 + 12.15 + 17.12 + 22.7 + 27.2}}{{44}} = \frac{{162}}{{11}}\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {9,5;14,5} \right)\).
Do đó, \({u_m} = 9,5,{u_{m + 1}} = 14,5,{n_m} = 15,{n_{m + 1}} = 12,{n_{m - 1}} = 8,{u_{m + 1}} - {u_m} = 14,5 - 9,5 = 5\)
Mốt của mẫu số liệu là: \({M_O} = 9,5 + \frac{{15 - 8}}{{\left( {15 - 8} \right) + \left( {15 - 12} \right)}}.5 = 13\)
b) Gọi \({x_1},{x_2},...,{x_{44}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_8} \in \left[ {4,5;9,5} \right),{x_9},...,{x_{23}} \in \left[ {9,5;14,5} \right),{x_{24}},...,{x_{35}} \in \left[ {14,5;19,5} \right),\) \({x_{36}},...,{x_{42}} \in \left[ {19,5;24,5} \right),{x_{43}},{x_{44}} \in \left[ {24,5;29,5} \right)\)
Do cỡ mẫu \(n = 44\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{11}} + {x_{12}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {9,5;14,5} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 9,5 + \frac{{\frac{{44}}{4} - \left( {8 + 0} \right)}}{{15}}.\left( {14,5 - 9,5} \right) = 10,5\)
Vậy giáo viên nên trao danh hiệu cho các gia đình không dùng quá 10 túi nhựa.
Giải bài 2 trang 161 Sách bài tập Toán 11 Chân trời sáng tạo tập 1: Tổng quan
Bài 2 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và thực hành thường xuyên là chìa khóa để giải quyết thành công bài tập này.
Nội dung bài 2 trang 161 Sách bài tập Toán 11 Chân trời sáng tạo tập 1
Bài 2 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, và các hàm số phức tạp hơn.
- Áp dụng quy tắc tính đạo hàm: Sử dụng các quy tắc như quy tắc cộng, trừ, nhân, chia, quy tắc chuỗi để tính đạo hàm.
- Tìm đạo hàm cấp hai: Tính đạo hàm bậc hai của hàm số.
- Ứng dụng đạo hàm: Giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số, cực trị của hàm số, và các bài toán tối ưu hóa.
Lời giải chi tiết bài 2 trang 161 Sách bài tập Toán 11 Chân trời sáng tạo tập 1
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài 2 trang 161, chúng tôi xin trình bày lời giải chi tiết như sau:
Ví dụ minh họa (Giả định bài 2 là tính đạo hàm của hàm số f(x) = x^3 + 2x^2 - 5x + 1)
Lời giải:
Để tính đạo hàm của hàm số f(x) = x^3 + 2x^2 - 5x + 1, ta áp dụng quy tắc tính đạo hàm của tổng và các hàm số đơn thức:
f'(x) = d/dx (x^3) + d/dx (2x^2) - d/dx (5x) + d/dx (1)
f'(x) = 3x^2 + 4x - 5 + 0
f'(x) = 3x^2 + 4x - 5
Vậy, đạo hàm của hàm số f(x) = x^3 + 2x^2 - 5x + 1 là f'(x) = 3x^2 + 4x - 5.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Sử dụng công cụ hỗ trợ: Sử dụng máy tính cầm tay hoặc các phần mềm tính đạo hàm để kiểm tra kết quả.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, hãy hỏi thầy cô giáo hoặc bạn bè để được hướng dẫn.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục kiến thức Toán học. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết, và các mẹo giải bài tập hiệu quả. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Bảng tổng hợp các công thức đạo hàm thường gặp
| Hàm số f(x) | Đạo hàm f'(x) |
|---|---|
| C (hằng số) | 0 |
| x^n | nx^(n-1) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |