Giải bài 1 trang 76 SBT Toán 11 Chân trời sáng tạo tập 2

Giải bài 1 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Giải bài 1 trang 76 sách bài tập Toán 11 Chân trời sáng tạo tập 2

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 76 một cách dễ hiểu nhất.

Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. a) \(BC \bot \left( {OAH} \right)\). b) H là trực tâm của \(\Delta ABC\). c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

Đề bài

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Chứng minh rằng:

a) \(BC \bot \left( {OAH} \right)\).

b) H là trực tâm của \(\Delta ABC\).

c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

Phương pháp giải - Xem chi tiết Giải bài 1 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2 1

Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng:

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).

+ Nếu đường thẳng d vuông góc với mặt phẳng \(\left( \alpha \right)\) thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng \(\left( \alpha \right)\).

Lời giải chi tiết

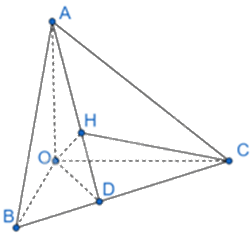
Giải bài 1 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2 2

a) Vì H là hình chiếu của O trên mặt phẳng (ABC) nên \(OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC\)

Vì \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {BOC} \right) \Rightarrow OA \bot BC\)

Ta có: \(OA \bot BC,OH \bot BC \Rightarrow BC \bot \left( {OAH} \right)\)

b) Vì \(BC \bot \left( {OAH} \right)\) nên \(BC \bot AH\) (1)

Vì \(OH \bot \left( {ABC} \right) \Rightarrow OH \bot AC\)

Vì \(OA \bot OB,OB \bot OC \Rightarrow OB \bot \left( {AOC} \right) \Rightarrow OB \bot AC\)

Ta có: \(OB \bot AC,OH \bot AC \Rightarrow AC \bot \left( {OBH} \right) \Rightarrow AC \bot BH\) (2)

Mà H là giao điểm của BH và CH (3)

Từ (1), (2) và (3) ta có: H là trực tâm của \(\Delta ABC\).

c) Gọi D là giao điểm của AH và BC. Khi đó, \(OD \bot BC\)

Vì \(OA \bot \left( {BOC} \right) \Rightarrow OA \bot OD\)

Do đó, tam giác AOD vuông tại O. Mà OH là đường cao nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{D^2}}} + \frac{1}{{O{A^2}}}\)

Tam giác BOC vuông tại O, đường cao OD có: \(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)

Vậy \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)

Giải bài 1 trang 76 SBT Toán 11 Chân trời sáng tạo tập 2: Tổng quan

Bài 1 trang 76 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về định nghĩa đạo hàm, các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp để giải quyết các bài toán cụ thể.

Nội dung bài tập

Bài 1 thường bao gồm các dạng bài tập sau:

Tính đạo hàm của hàm số tại một điểm cho trước.
Tìm đạo hàm của hàm số.
Xác định hệ số góc của tiếp tuyến của đồ thị hàm số tại một điểm.
Ứng dụng đạo hàm để giải các bài toán liên quan đến tốc độ thay đổi.

Lời giải chi tiết bài 1 trang 76

Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lưu ý rằng, trước khi bắt đầu giải bài tập, bạn cần nắm vững các kiến thức cơ bản về đạo hàm và các quy tắc tính đạo hàm.

Câu a: (Ví dụ minh họa)

Giả sử hàm số f(x) = x² + 2x - 1. Hãy tính f'(2).

Lời giải:

f'(x) = 2x + 2

f'(2) = 2(2) + 2 = 6

Câu b: (Ví dụ minh họa)

Giả sử hàm số g(x) = sin(x). Hãy tìm g'(x).

Lời giải:

g'(x) = cos(x)

Mẹo giải bài tập đạo hàm hiệu quả

Để giải các bài tập về đạo hàm một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:

Nắm vững định nghĩa đạo hàm và các quy tắc tính đạo hàm.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm tính đạo hàm.
Kiểm tra lại kết quả sau khi giải bài tập.

Tầm quan trọng của việc học đạo hàm

Đạo hàm là một khái niệm quan trọng trong toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật,... Việc nắm vững kiến thức về đạo hàm sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả hơn.

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

Tusach.vn là website chuyên cung cấp lời giải bài tập, tài liệu học tập cho học sinh các cấp. Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, chính xác và dễ hiểu nhất. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập của bạn!

Chủ đề	Nội dung
Định nghĩa đạo hàm	Tỷ số giữa độ biến thiên của hàm số và độ biến thiên của đối số khi đối số tiến tới một giá trị xác định.
Quy tắc tính đạo hàm	Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...
Nguồn: tusach.vn