Giải bài 5 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 5 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1
Bài 5 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hàm số và đồ thị hàm số. Bài tập này thường yêu cầu học sinh xác định tập xác định, tập giá trị, tính đơn điệu và vẽ đồ thị của hàm số.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\). a) Vẽ đồ thị của hàm số đã cho.
Đề bài
Cho hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
a) Vẽ đồ thị của hàm số đã cho.
b) Tìm các giá trị của \(x \in \left[ { - \frac{{7\pi }}{4};\frac{\pi }{4}} \right]\) sao cho \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\).
c) Tìm các giá trị của \(x \in \left[ { - \frac{{5\pi }}{6};\frac{\pi }{6}} \right]\) sao cho \(\tan \left( {2x + \frac{\pi }{6}} \right) \ge - \frac{{\sqrt 3 }}{3}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đồ thị hàm số \(y = \tan x\) để giải.
Lời giải chi tiết
a) Ta có đồ thị của hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\):
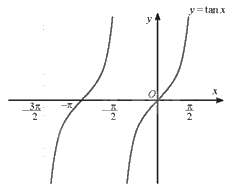
b) \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\) khi \(\tan \left( {x + \frac{\pi }{4}} \right) = \frac{{ - \sqrt 3 }}{3}\)
Đặt \(x + \frac{\pi }{4} = t\). Vì \(\frac{{ - 7\pi }}{4} \le x \le \frac{\pi }{4} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)
Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\).
Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:
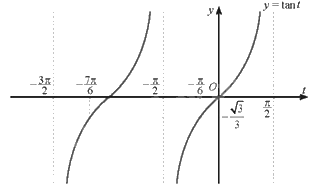
Từ đồ thị hàm số trên ta có:
\(\tan t = \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(t = \frac{{ - 7\pi }}{6}\) hoặc \(t = \frac{{ - \pi }}{6}\).
Suy ra: \(x + \frac{\pi }{4} = \frac{{ - 7\pi }}{6}\) hoặc \(x + \frac{\pi }{4} = \frac{{ - \pi }}{6}\). Do đó, \(x = \frac{{ - 17\pi }}{{12}}\) hoặc \(x = \frac{{ - 5\pi }}{{12}}\).
c) Đặt \(2x + \frac{\pi }{6} = t\). Vì \(\frac{{ - 5\pi }}{6} \le x \le \frac{\pi }{6} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)
Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\)
Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:
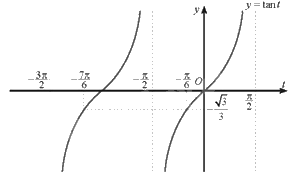
Từ đồ thị hàm số trên ta có:
\(\tan t \ge \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(\frac{{ - 7\pi }}{6} \le t < - \frac{\pi }{2}\) hoặc \(\frac{{ - \pi }}{6} \le t < \frac{\pi }{2}\).
Suy ra, \(\frac{{ - 7\pi }}{6} \le 2x + \frac{\pi }{6} < - \frac{\pi }{2}\) hoặc \(\frac{{ - \pi }}{6} \le 2x + \frac{\pi }{6} < \frac{\pi }{2}\)
Do đó, \(\frac{{ - 2\pi }}{3} \le x < - \frac{\pi }{3}\) hoặc \( - \frac{\pi }{6} \le x < \frac{\pi }{6}\).
Giải bài 5 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải
Bài 5 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
- Định nghĩa hàm số bậc hai: Hàm số có dạng y = ax2 + bx + c, với a ≠ 0.
- Tập xác định: Tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Tập giá trị: Tập hợp tất cả các giá trị của y mà hàm số có thể đạt được.
- Đỉnh của parabol: Điểm có tọa độ (x0, y0), với x0 = -b/2a và y0 là giá trị của hàm số tại x0.
- Trục đối xứng: Đường thẳng x = x0.
- Tính đơn điệu: Hàm số đồng biến hoặc nghịch biến trên các khoảng xác định.
Lời giải chi tiết bài 5 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1
Để cung cấp lời giải chính xác, cần biết nội dung cụ thể của bài 5 trang 27. Tuy nhiên, dưới đây là một ví dụ minh họa cách giải một bài tập tương tự:
Ví dụ: Giải bài tập về hàm số bậc hai
Cho hàm số y = x2 - 4x + 3. Hãy xác định:
- Tập xác định.
- Tập giá trị.
- Tọa độ đỉnh của parabol.
- Trục đối xứng.
- Tính đơn điệu.
Giải:
- Tập xác định: Vì hàm số là hàm đa thức, tập xác định là R.
- Tập giá trị: Hàm số có dạng parabol mở lên trên (a = 1 > 0), do đó tập giá trị là [y0; +∞). Tính y0: x0 = -(-4)/(2*1) = 2. y0 = 22 - 4*2 + 3 = -1. Vậy tập giá trị là [-1; +∞).
- Tọa độ đỉnh: (2; -1).
- Trục đối xứng: x = 2.
- Tính đơn điệu: Hàm số nghịch biến trên khoảng (-∞; 2) và đồng biến trên khoảng (2; +∞).
Mẹo giải nhanh và lưu ý quan trọng
Để giải nhanh các bài tập về hàm số bậc hai, bạn nên:
- Sử dụng công thức tính tọa độ đỉnh và trục đối xứng.
- Xác định dấu của hệ số a để biết parabol mở lên trên hay xuống dưới.
- Luyện tập thường xuyên để nắm vững các kỹ năng giải bài tập.
Ngoài ra, hãy chú ý đến các điều kiện của bài toán để đảm bảo lời giải chính xác và đầy đủ.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
tusach.vn là website cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm:
- Giải bài tập sách giáo khoa
- Giải bài tập sách bài tập
- Đề thi thử
- Bài giảng video
Hãy truy cập tusach.vn để học tập và ôn luyện Toán 11 hiệu quả!
| Công thức | Mô tả |
|---|---|
| x0 = -b/2a | Hoành độ đỉnh của parabol |
| y0 = f(x0) | Tung độ đỉnh của parabol |