Giải bài 1 trang 50 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Tổng quan nội dung
Giải bài 1 trang 50 SBT Toán 11 Chân trời sáng tạo tập 2
Chào mừng bạn đến với lời giải chi tiết bài 1 trang 50 sách bài tập Toán 11 Chân trời sáng tạo tập 2 trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM.
Đề bài
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai đường thẳng trong không gian để tính: Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b.
Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\).
Lời giải chi tiết
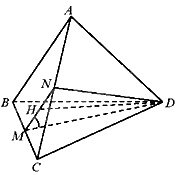
Gọi độ dài cạnh của tứ diện đều ABCD là 2a nên \(MB = MC = \frac{{BC}}{2} = a\)
Gọi N là trung điểm của AC nên \(NA = NC = \frac{{AC}}{2} = a\)
Vì MN là đường trung bình của tam giác ABC nên MN//AB
Do đó, \(\left( {AB,DM} \right) = \left( {MN,MD} \right) = \widehat {NMD}\)
Tam giác CBD đều nên MD là đường trung tuyến đồng thời là đường cao.
Do đó, \(MD \bot BC\). Áp dụng định lí Pythagore vào tam giác MDC vuông tại M có: \(MD = \sqrt {C{D^2} - M{C^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Tam giác ADC đều nên ND là đường trung tuyến đồng thời là đường cao.
Do đó, \(ND \bot AC\). Áp dụng định lí Pythagore vào tam giác NDC vuông tại N có: \(ND = \sqrt {C{D^2} - N{C^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Tam giác MND có: \(ND = MD\) nên tam giác MND cân tại D.
Gọi H là trung điểm của MN.
Suy ra DH là đường là đường trung tuyến đồng thời là đường cao của tam giác MND.
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{{BA}}{2} = a \Rightarrow MH = \frac{{MN}}{2} = \frac{a}{2}\)
Tam giác MHD vuông tại H có: \(\cos \widehat {HMD} = \frac{{MH}}{{MD}} = \frac{{\frac{a}{2}}}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{6} \Rightarrow \widehat {NMD} \approx 73,{2^0}\)
Giải bài 1 trang 50 SBT Toán 11 Chân trời sáng tạo tập 2: Tổng quan và Phương pháp giải
Bài 1 trang 50 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về Đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).
Nội dung chi tiết bài 1 trang 50 SBT Toán 11 Chân trời sáng tạo tập 2
Để giải quyết bài 1 trang 50 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Khái niệm đạo hàm: Hiểu rõ đạo hàm của một hàm số tại một điểm là gì và ý nghĩa của nó.
- Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản và các phép toán trên hàm số.
- Ứng dụng của đạo hàm: Biết cách sử dụng đạo hàm để giải quyết các bài toán liên quan đến tìm cực trị, khảo sát hàm số, và các bài toán thực tế.
Lời giải chi tiết bài 1 trang 50 SBT Toán 11 Chân trời sáng tạo tập 2
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 1 trang 50:
Câu a:
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Câu b:
Đề bài: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x)
Lời giải:
g'(x) = cos(x) - sin(x)
Câu c:
Đề bài: Tính đạo hàm của hàm số h(x) = ex + ln(x)
Lời giải:
h'(x) = ex + 1/x
Mẹo giải nhanh và hiệu quả
Để giải nhanh các bài tập về đạo hàm, bạn nên:
- Nắm vững bảng đạo hàm cơ bản: Điều này giúp bạn tiết kiệm thời gian và tránh sai sót.
- Sử dụng quy tắc tính đạo hàm một cách linh hoạt: Áp dụng đúng quy tắc cho từng hàm số và phép toán.
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự và luyện tập
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa và sách bài tập Toán 11. Chúng tôi hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 1 trang 50 SBT Toán 11 Chân trời sáng tạo tập 2. Chúc bạn học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |