Giải bài 5 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Tổng quan nội dung
Giải bài 5 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 68 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình chóp tam giác S.ABC có tam giác ABC vuông cân tại B, \(AC = a\sqrt 2 \), mặt phẳng (SAC) vuông góc với mặt đáy (ABC).
Đề bài
Cho hình chóp tam giác S.ABC có tam giác ABC vuông cân tại B, \(AC = a\sqrt 2 \), mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng \({60^0}\). Tính theo a thể tích V của khối chóp S. ABC
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)
Lời giải chi tiết
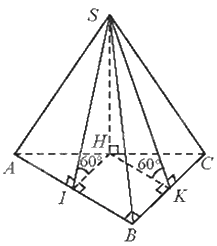
Trong mặt phẳng (SAC), vẽ \(SH \bot AC\left( {H \in AC} \right)\). Vì \(\left( {SAC} \right) \bot \left( {ABC} \right)\) và AC là giao tuyến của hai mặt phẳng (SAC) và (ABC) nên \(SH \bot \left( {ABC} \right)\).
Gọi I, K lần lượt là hình chiếu vuông góc của H lên AB và BC.
Khi đó, \(\left( {\left( {SAB} \right),\left( {ABC} \right)} \right) = \widehat {SIH} = {60^0}\), \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \widehat {SKH} = {60^0}\)
Chứng minh được \(\Delta SHI = \Delta SHK\left( {cgv - gn} \right) \) \(\Rightarrow HI = HK\)
Tứ giác BIHK có: \(\widehat {IBK} = \widehat {BKH} = \widehat {BIH} = {90^0}\) và \(HI = HK\) nên tứ giác BIHK là hình vuông. Suy ra, H là trung điểm của AC. Khi đó, tứ giác BIHK là hình vuông cạnh \(\frac{a}{2}\).
Tam giác SHI vuông tại H nên \(SH = HI.\tan \widehat {SIH} = \frac{{a\sqrt 3 }}{2}\)
Do đó, thể tích V của khối chóp S.ABC là: \(V = \frac{1}{3}{S_{\Delta ABC}}.SH = \frac{1}{3}.\frac{{{a^2}}}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Giải bài 5 trang 68 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2: Tổng quan
Bài 5 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương và đạo hàm hàm hợp. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung bài tập 5 trang 68
Bài tập 5 thường bao gồm các dạng câu hỏi sau:
- Tính đạo hàm của hàm số cho trước.
- Tìm đạo hàm cấp hai của hàm số.
- Xác định hệ số góc của tiếp tuyến tại một điểm trên đồ thị hàm số.
- Ứng dụng đạo hàm để giải các bài toán liên quan đến tốc độ thay đổi.
Lời giải chi tiết bài 5 trang 68
Để giải bài 5 trang 68 một cách hiệu quả, bạn cần:
- Xác định đúng các quy tắc đạo hàm cần sử dụng.
- Thực hiện các phép tính đạo hàm một cách cẩn thận, tránh sai sót.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 5 trang 68:
Câu a: (Ví dụ minh họa)
Cho hàm số f(x) = x3 + 2x2 - 5x + 1. Tính f'(x).
Lời giải:
f'(x) = 3x2 + 4x - 5
Câu b: (Ví dụ minh họa)
Cho hàm số g(x) = sin(x) * cos(x). Tính g'(x).
Lời giải:
g'(x) = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos2(x) - sin2(x)
Mẹo giải nhanh
Để tiết kiệm thời gian và nâng cao hiệu quả giải bài tập, bạn có thể áp dụng một số mẹo sau:
- Sử dụng bảng đạo hàm các hàm số cơ bản.
- Luyện tập thường xuyên để nắm vững các quy tắc đạo hàm.
- Chia nhỏ bài toán phức tạp thành các bước nhỏ hơn.
- Sử dụng máy tính cầm tay để kiểm tra kết quả.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự sau:
- Bài 1 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2
- Bài 2 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2
- Bài 3 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2
Kết luận
Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, bạn đã có thể tự tin giải bài 5 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2. Đừng quên luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong các kỳ thi.
Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.