Giải bài 4 trang 158 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 4 trang 158 SBT Toán 11 Chân trời sáng tạo tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 158 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Thầy giáo thống kê lại số lần kéo xà đơn của các học sinh nam khối 11 ở bảng sau: a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên. b) Thầy giáo dự định chọn 25% học sinh có số lần kéo thấp nhất để bồi dưỡng thể lực thêm. Thầy giáo nên chọn học sinh có thành tích kéo xà đơn dưới bao nhiêu lần để bồi dưỡng thể lực?
Đề bài
Thầy giáo thống kê lại số lần kéo xà đơn của các học sinh nam khối 11 ở bảng sau:

a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Thầy giáo dự định chọn 25% học sinh có số lần kéo thấp nhất để bồi dưỡng thể lực thêm. Thầy giáo nên chọn học sinh có thành tích kéo xà đơn dưới bao nhiêu lần để bồi dưỡng thể lực?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
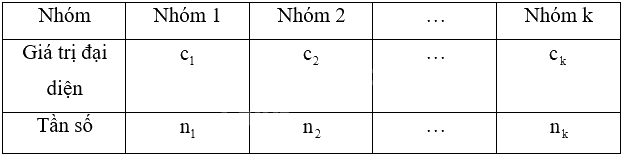
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
b) Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Lời giải chi tiết
Ta hiệu chỉnh lại bảng số liệu bao gồm giá trị đại diện:

Cỡ mẫu \(n = 143\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{8.35 + 13.54 + 18.32 + 23.17 + 28.5}}{{143}} = \frac{{2\;089}}{{143}}\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {10,5;15,5} \right)\).
Do đó, \({u_m} = 10,5,{u_{m + 1}} = 15,5,{n_m} = 54,{n_{m - 1}} = 35,{n_{m + 1}} = 32,{u_{m + 1}} - {u_m} = 15,5 - 10,5 = 5\)
Mốt của mẫu số liệu là: \({M_O} = 10,5 + \frac{{54 - 35}}{{\left( {54 - 35} \right) + \left( {54 - 32} \right)}}.5 = \frac{{1051}}{{82}}\).
Gọi \({x_1},{x_2},...,{x_{143}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{35}} \in \left[ {5,5;10,5} \right),{x_{36}},...,{x_{89}} \in \left[ {10,5;15,5} \right),{x_{90}},...,{x_{121}} \in \left[ {15,5;20,5} \right),\)\({x_{122}},...,{x_{138}} \in \left[ {20,5;25,5} \right),{x_{139}},...,{x_{143}} \in \left[ {25,5;30,5} \right)\)
Do cỡ mẫu \(n = 143\) nên trung vị \({M_e} = {x_{72}} \in \left[ {10,5;15,5} \right)\) nên trung vị của mẫu số liệu là:
\({M_e} = 10,5 + \frac{{\frac{{143}}{2} - 35}}{{54}}.\left( {15,5 - 10,5} \right) = \frac{{1499}}{{108}}\)
b) Do cỡ mẫu \(n = 143\) nên tứ phân vị thứ nhất của mẫu số liệu là \({x_{36}}\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {10,5;15,5} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 10,5 + \frac{{\frac{{143}}{4} - \left( {35 + 0} \right)}}{{54}}.\left( {15,5 - 10,5} \right) = \frac{{761}}{{72}} \approx 10,57\)
Vậy giáo viên nên chọn các bạn có thành tích kéo xà dưới 11 lần để bồi dưỡng thể lực thêm.
Giải bài 4 trang 158 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan
Bài 4 trang 158 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm là yếu tố then chốt để hoàn thành tốt bài tập này.
Nội dung bài 4 trang 158 SBT Toán 11 Chân trời sáng tạo tập 1
Bài 4 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số tại một điểm cho trước.
- Tìm đạo hàm của hàm số.
- Vận dụng đạo hàm để giải các bài toán liên quan đến vận tốc, gia tốc, hoặc các bài toán tối ưu hóa.
Lời giải chi tiết bài 4 trang 158 SBT Toán 11 Chân trời sáng tạo tập 1
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng phần của bài 4:
Câu a: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế của bài 4)
Cho hàm số f(x) = x2 + 2x + 1. Tính f'(2).
Giải:
f'(x) = 2x + 2
f'(2) = 2 * 2 + 2 = 6
Câu b: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế của bài 4)
Tìm đạo hàm của hàm số g(x) = sin(x) + cos(x).
Giải:
g'(x) = cos(x) - sin(x)
Mẹo giải bài tập đạo hàm Toán 11
Để giải tốt các bài tập về đạo hàm, các em nên:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các quy tắc đạo hàm như quy tắc tích, quy tắc thương, quy tắc chuỗi một cách linh hoạt.
- Kiểm tra lại kết quả sau khi tính đạo hàm.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
- Các trang web học toán trực tuyến như Tusach.vn.
- Các video bài giảng về đạo hàm trên YouTube.
- Các diễn đàn học tập trực tuyến.
Kết luận
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin hơn khi giải bài 4 trang 158 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các em học tập tốt!
| Công thức đạo hàm | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x3)' = 3x2 |
| (sin x)' = cos x | (sin x)' = cos x |