Giải bài 4 trang 133 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 4 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 trên tusach.vn. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và nhanh chóng nhất để hỗ trợ các em trong quá trình học tập.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và tam giác SAB đều. Gọi M là điểm thuộc cạnh BC sao cho \(BM = x\left( {0 < x < a} \right)\), mặt phẳng \(\left( \alpha \right)\) đi qua M song song với hai đường thẳng SA và AB. a) Xác định giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp. b) Tính diện tích hình tạo bởi các đoạn giao tuyến ở câu a theo a và x.
Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và tam giác SAB đều. Gọi M là điểm thuộc cạnh BC sao cho \(BM = x\left( {0 < x < a} \right)\), mặt phẳng \(\left( \alpha \right)\) đi qua M song song với hai đường thẳng SA và AB.
a) Xác định giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
b) Tính diện tích hình tạo bởi các đoạn giao tuyến ở câu a theo a và x.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để tìm giao tuyến: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết
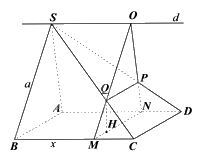
a) Trong mặt phẳng (ABCD), kẻ MN//AB//CD (N thuộc AD)
Trong mặt phẳng (SAD), kẻ đường thẳng d đi qua S và song song với AD. Qua N kẻ đường thẳng song song với SA cắt d tại O.
Gọi P là giao điểm của NO và SD, Q là giao điểm của MO và SC.
Khi đó, \(\left( \alpha \right)\) là mặt phẳng (OMN).
Ta có:
\(\left( \alpha \right) \cap \left( {ABCD} \right) = MN,\left( \alpha \right) \cap \left( {SBC} \right) = MQ,\left( \alpha \right) \cap \left( {SCD} \right) = PQ,\left( \alpha \right) \cap \left( {ASD} \right) = PN.\)
b) Các giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp tạo thành tứ giác MNPQ.
Vì CD//MN//PQ nên tứ giác MNPQ là hình thang với \(MN = AB = a,\widehat {QMN} = \widehat {SBA} = {60^0}\)
Trong tam giác SBC có MQ//SB nên theo hệ quả định lí Thalès ta có: \(\frac{{MQ}}{{SB}} = \frac{{MC}}{{BC}}\)
Mà \(SB = BC \Rightarrow MQ = MC = a - x\)
Trong tam giác SDC có PQ//CD nên theo hệ quả định lí Thalès ta có: \(\frac{{PQ}}{{CD}} = \frac{{SQ}}{{SC}}\)
Trong tam giác SBC có MQ//SB nên theo định lí Thalès ta có: \(\frac{{SQ}}{{SC}} = \frac{{MB}}{{BC}}\)
Do đó, \(\frac{{PQ}}{{CD}} = \frac{{BM}}{{BC}}\), mà \(CD = BC \Rightarrow QP = BM = x\)
Qua Q kẻ đường thẳng vuông góc với MN cắt MN tại H.
Ta có: \(\widehat {SBA} = \widehat {HMQ} = {60^0}\)
Khi đó, \(QH = MQ.\sin \widehat {QMH} = MQ.\sin {60^0} = \frac{{\left( {a - x} \right)\sqrt 3 }}{2}\)
Vậy diện tích hình thang MNPQ là: \(S = \frac{1}{2}QH\left( {MN + PQ} \right) = \frac{1}{2}.\frac{{\left( {a - x} \right)\sqrt 3 }}{2}\left( {a + x} \right) = \frac{{\left( {{a^2} - {x^2}} \right)\sqrt 3 }}{4}\) (đvdt)
Giải bài 4 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan
Bài 4 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về Đạo hàm của hàm số. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm cơ bản, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số, cũng như đạo hàm của hàm hợp. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chi tiết bài 4 trang 133
Bài 4 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước, có thể là hàm đơn thức, đa thức, hoặc hàm hợp.
- Tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm cấp hai của một hàm số, tức là đạo hàm của đạo hàm cấp nhất.
- Ứng dụng đạo hàm để giải phương trình: Sử dụng đạo hàm để tìm nghiệm của phương trình hoặc bất phương trình.
- Bài toán thực tế: Một số bài tập có thể liên hệ với các bài toán thực tế, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết.
Lời giải chi tiết bài 4 trang 133
Dưới đây là lời giải chi tiết cho từng phần của bài 4 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1:
Câu a)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Câu b)
Đề bài: Tính đạo hàm của hàm số g(x) = (x2 + 1)(x - 2)
Lời giải:
g'(x) = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Câu c)
Đề bài: Tính đạo hàm của hàm số h(x) = sin(2x)
Lời giải:
h'(x) = cos(2x) * 2 = 2cos(2x)
Mẹo giải bài tập đạo hàm hiệu quả
- Nắm vững các quy tắc tính đạo hàm: Đây là yếu tố then chốt để giải quyết mọi bài tập về đạo hàm.
- Phân tích cấu trúc hàm số: Xác định hàm số là đơn thức, đa thức, hàm hợp hay hàm lượng giác để áp dụng quy tắc phù hợp.
- Thực hành thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 11. Chúng tôi luôn cập nhật những nội dung mới nhất và hỗ trợ học sinh tối đa trong quá trình học tập. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của hằng số | (c)' = 0 |
| Đạo hàm của xn | (xn)' = nxn-1 |
| Đạo hàm của tổng/hiệu | (u ± v)' = u' ± v' |
| Bảng tổng hợp một số quy tắc đạo hàm cơ bản | |