Giải bài 3 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 3 trang 112 sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải chi tiết, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh rằng ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Đề bài
Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh rằng ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về chứng minh ba đường thẳng đồng quy để chứng minh ba đường thẳng đồng quy:
+ Gọi O là giao điểm của HF và IG
+ Chứng minh O thuộc CD.
Lời giải chi tiết
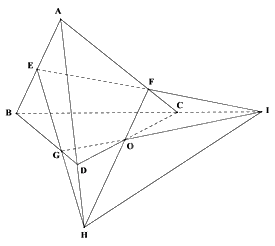
Gọi O là giao điểm của HF và IG.
Ta có: \(O \in HF\), mà \(HF \subset \left( {ACD} \right) \Rightarrow O \in \left( {ACD} \right)\)
Vì \(O \in IG\), mà \(IG \subset \left( {BCD} \right) \Rightarrow O \in \left( {BCD} \right)\)
Do đó, \(O \in \left( {BCD} \right) \cap \left( {ACD} \right)\)
Mặt khác, CD là giao tuyến của hai mặt phẳng (ACD) và (BCD)
Do đó, \(O \in CD\). Vậy ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Giải bài 3 trang 112 Sách bài tập Toán 11 Chân trời sáng tạo tập 1: Tổng quan
Bài 3 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về Đạo hàm của hàm số. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm cơ bản để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức về đạo hàm là vô cùng quan trọng, không chỉ cho việc giải các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình Toán học.
Nội dung bài tập
Bài 3 trang 112 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số đơn thức, đa thức.
- Tính đạo hàm của hàm số lượng giác.
- Tính đạo hàm của hàm số hợp.
- Áp dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.
Lời giải chi tiết bài 3 trang 112
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 3 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1:
Câu a)
Đề bài: Tính đạo hàm của hàm số f(x) = 3x2 + 5x - 2
Lời giải:
f'(x) = d/dx (3x2) + d/dx (5x) - d/dx (2)
f'(x) = 6x + 5 - 0
f'(x) = 6x + 5
Câu b)
Đề bài: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x)
Lời giải:
g'(x) = d/dx (sin(x)) + d/dx (cos(x))
g'(x) = cos(x) - sin(x)
Câu c)
Đề bài: Tính đạo hàm của hàm số h(x) = (x2 + 1)3
Lời giải:
Áp dụng quy tắc chuỗi: h'(x) = 3(x2 + 1)2 * d/dx (x2 + 1)
h'(x) = 3(x2 + 1)2 * 2x
h'(x) = 6x(x2 + 1)2
Mẹo giải bài tập đạo hàm
Để giải các bài tập về đạo hàm một cách hiệu quả, các em nên:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng quy tắc chuỗi một cách linh hoạt khi gặp các hàm số hợp.
- Kiểm tra lại kết quả sau khi tính đạo hàm.
Tài liệu tham khảo thêm
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
- Các trang web học Toán trực tuyến như tusach.vn.
- Các video bài giảng về đạo hàm trên YouTube.
- Các diễn đàn trao đổi kiến thức Toán học.
Kết luận
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin hơn khi giải bài 3 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các em học tập tốt!