Giải bài 2 trang 117 SBT Toán 11 - Chân trời sáng tạo tập 1

Giải bài 2 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 2 trang 117 SBT Toán 11 Chân trời sáng tạo tập 1

Bài 2 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); I, J lần lượt là trung điểm của BD, CD. a) Chứng minh rằng MN//BC. b) Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.

Đề bài

Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); I, J lần lượt là trung điểm của BD, CD.

a) Chứng minh rằng MN//BC.

b) Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.

Phương pháp giải - Xem chi tiết Giải bài 2 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Lời giải chi tiết

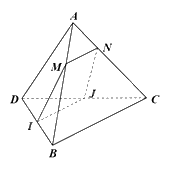
Giải bài 2 trang 117 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

a) Tam giác ABC có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên MN//BC (định lí Thalès đảo)

b) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Do đó, IJ//BC

Mà MN//BC nên IJ//MN, do đó, MNJI là hình thang.

Hình thang MNJI là hình bình hành khi và chỉ khi MI//NJ//AD.

Mà I là trung điểm của BD. Do đó, MI là đường trung bình của tam giác ADB.

Suy ra M là trung điểm của AB.

Giải bài 2 trang 117 SBT Toán 11 Chân trời sáng tạo tập 1: Chi tiết và Dễ hiểu

Bài 2 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1 yêu cầu chúng ta tìm cực trị của hàm số. Để giải bài này, chúng ta cần nắm vững các bước sau:

Tìm tập xác định của hàm số: Xác định miền giá trị mà hàm số có thể nhận.
Tính đạo hàm bậc nhất: Sử dụng các quy tắc đạo hàm để tìm đạo hàm f'(x) của hàm số.
Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng không.
Lập bảng biến thiên: Xác định dấu của đạo hàm f'(x) trên các khoảng xác định bởi các điểm dừng.
Kết luận về cực trị: Dựa vào bảng biến thiên, xác định các điểm cực đại, cực tiểu của hàm số.

Lời giải chi tiết bài 2 trang 117 SBT Toán 11 Chân trời sáng tạo tập 1

Đề bài: Tìm cực trị của các hàm số sau:

a) y = x³ - 3x² + 2

b) y = -x⁴ + 4x² - 1

Giải:

a) y = x³ - 3x² + 2

Tập xác định: D = ℝ
Đạo hàm bậc nhất: y' = 3x² - 6x
Điểm dừng: 3x² - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Bảng biến thiên:
x -∞ 0 2 +∞
y' + - +
y ↗ ↘ ↗
Kết luận: Hàm số đạt cực đại tại x = 0, y_CĐ = 2 và đạt cực tiểu tại x = 2, y_CT = -2

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

b) y = -x⁴ + 4x² - 1

Tập xác định: D = ℝ
Đạo hàm bậc nhất: y' = -4x³ + 8x
Điểm dừng: -4x³ + 8x = 0 ⇔ -4x(x² - 2) = 0 ⇔ x = 0, x = √2, x = -√2
Bảng biến thiên: (Tương tự như phần a, bạn tự lập bảng biến thiên)
Kết luận: Hàm số đạt cực đại tại x = -√2 và x = √2, đạt cực tiểu tại x = 0.

Mẹo giải nhanh và hiệu quả

Để giải nhanh các bài toán tìm cực trị, bạn nên:

Nắm vững các quy tắc đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.

Tusach.vn – Đồng hành cùng bạn học Toán 11

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 1. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập!