Giải bài 13 trang 10 SBT Toán 11 Chân trời sáng tạo tập 1
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu bài 13 trang 10 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải toán, chuẩn bị tốt cho các bài kiểm tra và kỳ thi sắp tới.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
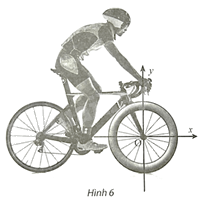
Trong chặng đua nước rút, bánh xe của một vận động viên đua xe đạp quay được 30 vòng trong 8 giây. Chọn chiều quay của bánh xe là chiều dương. Xét van V của bánh xe.
a) Sau 1 phút, van V đó quay được một góc có số đo bao nhiêu radian?
Giải bài 13 trang 10 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan
Bài 13 trang 10 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về Hàm số lượng giác. Bài tập này thường tập trung vào việc vận dụng các kiến thức về định nghĩa, tính chất của hàm số lượng giác, đồ thị hàm số lượng giác và các phép biến đổi hàm số lượng giác để giải quyết các bài toán cụ thể.
Nội dung chi tiết bài 13 trang 10 SBT Toán 11 Chân trời sáng tạo tập 1
Bài 13 thường bao gồm các dạng bài tập sau:
- Xác định tập xác định của hàm số lượng giác: Yêu cầu học sinh xác định khoảng giá trị của x để hàm số có nghĩa.
- Tìm tập giá trị của hàm số lượng giác: Xác định khoảng giá trị mà hàm số có thể đạt được.
- Khảo sát sự biến thiên của hàm số lượng giác: Xác định khoảng đồng biến, nghịch biến, cực trị của hàm số.
- Vẽ đồ thị hàm số lượng giác: Sử dụng các kiến thức về đồ thị hàm số để vẽ chính xác đồ thị của hàm số.
- Giải phương trình lượng giác: Sử dụng các công thức lượng giác và phương pháp giải phương trình để tìm nghiệm của phương trình.
Lời giải chi tiết bài 13 trang 10 SBT Toán 11 Chân trời sáng tạo tập 1
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 13 trang 10 sách bài tập Toán 11 Chân trời sáng tạo tập 1:
Câu 1: (Ví dụ minh họa)
Đề bài: Xác định tập xác định của hàm số y = tan(2x + π/3)
Lời giải: Hàm số y = tan(2x + π/3) xác định khi và chỉ khi 2x + π/3 ≠ π/2 + kπ (k ∈ Z). Giải phương trình này, ta được x ≠ π/12 + kπ/2 (k ∈ Z). Vậy tập xác định của hàm số là D = R \ {π/12 + kπ/2 | k ∈ Z}.
Câu 2: (Ví dụ minh họa)
Đề bài: Tìm tập giá trị của hàm số y = 2sin(x) + 1
Lời giải: Vì -1 ≤ sin(x) ≤ 1, nên -2 ≤ 2sin(x) ≤ 2. Do đó, -1 ≤ 2sin(x) + 1 ≤ 3. Vậy tập giá trị của hàm số là [-1; 3].
Mẹo giải bài tập Hàm số lượng giác
Để giải tốt các bài tập về hàm số lượng giác, bạn nên:
- Nắm vững các định nghĩa, tính chất và công thức lượng giác cơ bản.
- Luyện tập vẽ đồ thị hàm số lượng giác để hiểu rõ tính chất của chúng.
- Sử dụng các phương pháp giải phương trình lượng giác một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.
Tài liệu tham khảo thêm
Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 11
- Các trang web học toán trực tuyến
- Các video bài giảng về hàm số lượng giác
Tusach.vn hy vọng với lời giải chi tiết và những chia sẻ trên, bạn sẽ tự tin hơn trong việc giải bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc bạn học tốt!
