Giải bài 1 trang 133 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 1 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 133 SBT Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Cho hình bình hành ABCD. Từ các đỉnh A, B, C và D lần lượt kẻ các tia Ax, By, Cz, Dt song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt).
Đề bài
Cho hình bình hành ABCD. Từ các đỉnh A, B, C và D lần lượt kẻ các tia Ax, By, Cz, Dt song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết
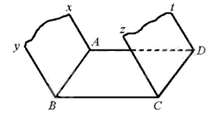
Vì Cz//By, \(By \subset \left( {Ax,By} \right)\), Cz không nằm trong mặt phẳng (Ax, By) nên Cz// (Ax, By).
Vì tứ giác ABCD là hình bình hành nên AB//CD. Mà \(AB \subset \left( {Ax,By} \right)\), CD không nằm trong mặt phẳng (Ax, By) nên CD// (Ax, By).
Vì Cz// (Ax, By), CD// (Ax, By), Cz và CD cắt nhau tại C và nằm trong mặt phẳng (Cz, Dt) nên (Cz, Dt) // (Ax, By).
Giải bài 1 trang 133 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan
Bài 1 trang 133 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về Đạo hàm của hàm số. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm cơ bản để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Nội dung bài tập
Bài 1 yêu cầu học sinh thực hiện các phép tính đạo hàm của các hàm số được cho. Các hàm số này có thể bao gồm các hàm số đơn giản như đa thức, hàm lượng giác, hoặc các hàm số phức tạp hơn được xây dựng từ các hàm số đơn giản thông qua các phép toán cộng, trừ, nhân, chia.
Phương pháp giải
Để giải bài 1 trang 133, học sinh cần:
- Nắm vững các quy tắc tính đạo hàm cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit, và các quy tắc cộng, trừ, nhân, chia đạo hàm.
- Xác định đúng các hàm số thành phần: Trong các hàm số phức tạp, cần xác định rõ các hàm số thành phần để áp dụng quy tắc đạo hàm hợp.
- Thực hiện các phép tính đạo hàm một cách cẩn thận: Tránh các lỗi sai do tính toán nhầm hoặc áp dụng sai quy tắc.
Lời giải chi tiết
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 1:
Câu a)
Hàm số: y = 3x2 - 5x + 2
Đạo hàm: y' = 6x - 5
Giải thích: Áp dụng quy tắc đạo hàm của hàm đa thức, ta có đạo hàm của 3x2 là 6x, đạo hàm của -5x là -5, và đạo hàm của 2 (hằng số) là 0.
Câu b)
Hàm số: y = sin(x) + cos(x)
Đạo hàm: y' = cos(x) - sin(x)
Giải thích: Áp dụng quy tắc đạo hàm của hàm sin và cos, ta có đạo hàm của sin(x) là cos(x) và đạo hàm của cos(x) là -sin(x).
Câu c)
Hàm số: y = ex + ln(x)
Đạo hàm: y' = ex + 1/x
Giải thích: Áp dụng quy tắc đạo hàm của hàm mũ và hàm logarit, ta có đạo hàm của ex là ex và đạo hàm của ln(x) là 1/x.
Lưu ý quan trọng
- Luôn kiểm tra lại kết quả đạo hàm để đảm bảo tính chính xác.
- Thực hành nhiều bài tập khác nhau để nắm vững các quy tắc tính đạo hàm.
- Sử dụng máy tính cầm tay hoặc các công cụ trực tuyến để kiểm tra kết quả.
Bài tập tương tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = 2x3 - x2 + 4x - 1
- Tính đạo hàm của hàm số y = tan(x) + cot(x)
- Tính đạo hàm của hàm số y = 2x + log2(x)
Kết luận
Bài 1 trang 133 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ hiểu rõ hơn về nội dung bài học và tự tin giải quyết các bài tập tương tự.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với Tusach.vn để được hỗ trợ.