Giải bài 1 trang 112 SBT Toán 11 - Chân trời sáng tạo tập 1

Giải bài 1 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 1 trang 112 SBT Toán 11 Chân trời sáng tạo tập 1

Tusach.vn xin giới thiệu đến quý học sinh lời giải chi tiết bài 1 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất, hỗ trợ các em học sinh học tập hiệu quả.

Cho hình chóp S. ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD. a) Tìm giao điểm EF với (SAC). b) Tìm giao điểm BC với (AEF).

Đề bài

Cho hình chóp S. ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD.

a) Tìm giao điểm EF với (SAC).

b) Tìm giao điểm BC với (AEF).

Phương pháp giải - Xem chi tiết Giải bài 1 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về giao điểm giữa đường thẳng và mặt phẳng để tìm: Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\):

- Trường hợp 1: Trong mặt phẳng \(\left( \alpha \right)\) có sẵn đường thẳng d’ cắt d tại I: Ta có ngay \(d \cap \left( \alpha \right) = I\)

- Trường hợp 2: Trong mặt phẳng \(\left( \alpha \right)\) không có sẵn đường thẳng d’ cắt d. Khi đó ta thực hiện như sau:

+ Chọn mặt phẳng phụ \(\left( \beta \right)\) chứa d và \(\left( \beta \right)\) cắt \(\left( \alpha \right)\) theo giao tuyến d’.

+ Gọi \(I = d' \cap d\). Khi đó, \(d \cap \left( \alpha \right) = I\).

Lời giải chi tiết

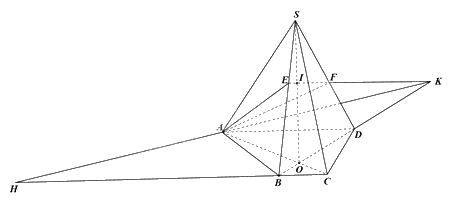
Giải bài 1 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

a) Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD. Do đó, SO là giao tuyến của mặt phẳng (SAC) và (SBD).

Trong mặt phẳng (SBD), gọi I là giao điểm của EF và SO.

Vì I thuộc EF, \(I \in SO \subset \left( {SAC} \right)\) nên I là giao điểm của EF và (SAC).

b) Trong mặt phẳng (SBD), gọi K là giao điểm của EF và BD. Khi đó, AK là giao tuyến của (ABCD) và (AEF).

Trong mặt phẳng (ABCD), gọi H là giao điểm của BC và AK.

Vì H thuộc BC, \(H \in AK \subset \left( {AEF} \right)\) nên H là giao điểm của BC và (AEF).

Giải bài 1 trang 112 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan

Bài 1 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản (sin, cos, tan, cot), tính chất của chúng, và các công thức lượng giác để giải quyết các bài toán cụ thể.

Nội dung chi tiết bài 1

Bài 1 thường bao gồm các dạng bài tập sau:

Xác định tập xác định của hàm số lượng giác: Học sinh cần xác định điều kiện để hàm số có nghĩa, dựa trên các mẫu số khác 0 và các biểu thức trong căn bậc chẵn lớn hơn hoặc bằng 0.
Tìm tập giá trị của hàm số lượng giác: Sử dụng kiến thức về khoảng giá trị của các hàm sin, cos, tan, cot để xác định tập giá trị của hàm số.
Xét tính chẵn, lẻ của hàm số lượng giác: Kiểm tra xem hàm số có thỏa mãn điều kiện f(-x) = f(x) (hàm chẵn) hay f(-x) = -f(x) (hàm lẻ) hay không.
Tìm chu kỳ của hàm số lượng giác: Sử dụng công thức chu kỳ của các hàm sin, cos, tan, cot để tìm chu kỳ của hàm số.
Vẽ đồ thị hàm số lượng giác: Biến đổi hàm số về dạng cơ bản và vẽ đồ thị dựa trên các điểm đặc biệt và tính chất của hàm số.

Lời giải chi tiết bài 1 trang 112 SBT Toán 11 Chân trời sáng tạo tập 1

Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 1:

Câu a)

Đề bài: (Ví dụ về đề bài câu a)

Lời giải: (Giải thích chi tiết từng bước giải câu a, kèm theo các công thức và lý thuyết liên quan)

Câu b)

Đề bài: (Ví dụ về đề bài câu b)

Lời giải: (Giải thích chi tiết từng bước giải câu b, kèm theo các công thức và lý thuyết liên quan)

Câu c)

Đề bài: (Ví dụ về đề bài câu c)

Lời giải: (Giải thích chi tiết từng bước giải câu c, kèm theo các công thức và lý thuyết liên quan)

Mẹo giải bài tập hàm số lượng giác

Để giải tốt các bài tập về hàm số lượng giác, bạn nên:

Nắm vững định nghĩa và tính chất của các hàm số lượng giác: Hiểu rõ khoảng giá trị, tập xác định, tính chẵn lẻ, chu kỳ của từng hàm số.
Thành thạo các công thức lượng giác cơ bản: Sử dụng các công thức cộng, trừ, nhân, chia góc, công thức hạ bậc, nâng bậc, và các công thức biến đổi lượng giác khác.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác các giá trị lượng giác.

Tài liệu tham khảo thêm

Để học tốt hơn về hàm số lượng giác, bạn có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 11
Sách bài tập Toán 11
Các trang web học Toán trực tuyến
Các video bài giảng về hàm số lượng giác

Tusach.vn hy vọng với lời giải chi tiết và những chia sẻ trên, các em học sinh sẽ hiểu rõ hơn về bài 1 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 và đạt kết quả tốt trong học tập.