Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh:
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP);
d) Gọi \({G_1}\) và \({G_2}\) theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh \({G_1}{G_2}\) song song với (SAD).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
Lời giải chi tiết
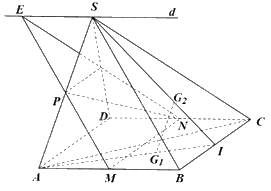
a) Hình bình hành ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD nên MN//AD//BC.
Ta có: MN//BC, \(BC \subset \left( {SBC} \right)\) và MN không nằm trong mặt phẳng (SBC) nên MN// (SBC).
Lại có: MN//AD, \(AD \subset \left( {SAD} \right)\) và MN không nằm trong mặt phẳng (SAD) nên MN// (SAD).
b) Vì P, M lần lượt là trung điểm của SA, AB nên PM là đường trung bình của tam giác SAB. Do đó, PM//SB. Mà \(PM \subset \left( {MNP} \right)\), SB không nằm trong mặt phẳng (MNP) nên SB//(MNP).
c) Trong mặt phẳng (SAB), vẽ đường thẳng d đi qua S và song song với AB.
Gọi E là giao điểm của MP và d.
Ta có: ES//AB, mà AB//CD nên ES//DC hay ES//NC (1)
Vì ES//MB, EM//SB nên tứ giác MBSE là hình bình hành, suy ra \(ES = MB\)
Mà \(MB = NC\) (vì M, N lần lượt là trung điểm của AB, DC và \(AB = DC\)), suy ra: \(ES = NC\) (2)
Từ (1) và (2) suy ra tứ giác ESCN là hình bình hành nên SC//NE.
Mà \(NE \subset \left( {MNP} \right)\), SC không nằm trong mặt phẳng (MNP) nên SC//(MNP).
d) Gọi I là trung điểm của BC.
Vì \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác ABC và SBC nên \(\frac{{I{G_1}}}{{IA}} = \frac{{I{G_2}}}{{IS}} = \frac{1}{3}\).
Tam giác SIA có: \(\frac{{I{G_1}}}{{IA}} = \frac{{I{G_2}}}{{IS}} = \frac{1}{3}\) nên \({G_1}{G_2}//SA\) (định lí Thalès đảo)
Mà \(SA \subset \left( {SAD} \right)\), \({G_1}{G_2}\) không nằm trong mặt phẳng (SAD) nên \({G_1}{G_2}//\left( {SAD} \right)\).
