Giải bài 4 trang 150 SBT Toán 11 - Chân trời sáng tạo tập 1

Giải bài 4 trang 150 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 4 trang 150 SBT Toán 11 Chân trời sáng tạo tập 1

Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 150 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án, hướng dẫn giải chi tiết và các kiến thức liên quan để giúp các em hiểu rõ hơn về nội dung bài học.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.

Bảng sau thống kê cân nặng (đơn vị: kg) của một số con ngan đực 88 ngày tuổi ở một trang trại. a) Hãy lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \(\left[ {4,6;4,7} \right)\). b) Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.

Đề bài

Bảng sau thống kê cân nặng (đơn vị: kg) của một số con ngan đực 88 ngày tuổi ở một trang trại.

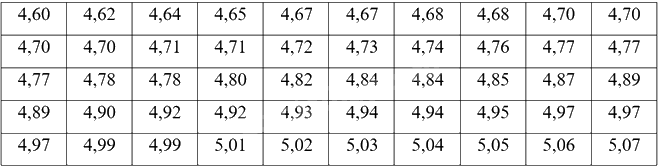
Giải bài 4 trang 150 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

a) Hãy lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \(\left[ {4,6;4,7} \right)\).

b) Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.

Phương pháp giải - Xem chi tiết Giải bài 4 trang 150 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

+ Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:

Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:

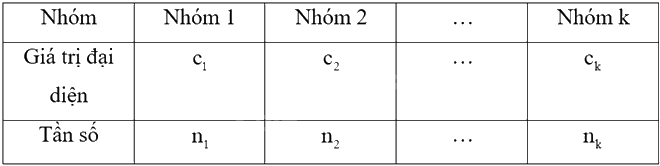
Giải bài 4 trang 150 sách bài tập toán 11 - Chân trời sáng tạo tập 1 3

Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).

+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)

Lời giải chi tiết

a) Bảng tần số ghép nhóm của mẫu số liệu:

Giải bài 4 trang 150 sách bài tập toán 11 - Chân trời sáng tạo tập 1 4

b) Bảng tần số ghép nhóm bao gồm các giá trị đại diện của nhóm là:

Giải bài 4 trang 150 sách bài tập toán 11 - Chân trời sáng tạo tập 1 5

Số trung bình của mẫu số liệu ghép nhóm là:

\(\overline x = \frac{{4,65.8 + 4,75.15 + 4,85.8 + 4,95.12 + 5,05.7}}{{8 + 15 + 8 + 12 + 7}} = 4,84\left( {kg} \right)\)

Nhóm chứa mốt của mẫu số liệu là \(\left[ {4,7;4,8} \right)\).

Do đó, \({u_m} = 4,7;{n_{m - 1}} = 8;{n_m} = 15,{n_{m + 1}} = 8,{u_{m + 1}} - {u_m} = 4,8 - 4,7 = 0,1\)

Mốt của mẫu số liệu ghép nhóm là: \({M_O} = 4,7 + \frac{{15 - 8}}{{\left( {15 - 8} \right) + \left( {15 - 8} \right)}}.0,1 = 4,75\)

Giải bài 4 trang 150 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan và Hướng dẫn chi tiết

Bài 4 trang 150 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về phép biến hình. Bài tập này thường tập trung vào việc vận dụng các kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán hình học cụ thể.

Nội dung chính của bài 4 trang 150 SBT Toán 11 Chân trời sáng tạo tập 1

Bài 4 thường yêu cầu học sinh:

Xác định ảnh của một điểm, một đường thẳng hoặc một hình qua một phép biến hình cho trước.
Tìm tâm, góc, trục hoặc mặt phẳng của một phép biến hình.
Chứng minh một hình là ảnh của một hình khác qua một phép biến hình.
Vận dụng các phép biến hình để giải quyết các bài toán hình học.

Hướng dẫn giải chi tiết bài 4 trang 150 SBT Toán 11 Chân trời sáng tạo tập 1

Để giải bài 4 trang 150 SBT Toán 11 Chân trời sáng tạo tập 1 một cách hiệu quả, các em cần nắm vững các kiến thức sau:

Phép tịnh tiến: Biến đổi mỗi điểm thành một điểm sao cho đoạn thẳng nối hai điểm tương ứng song song và bằng nhau.
Phép quay: Biến đổi mỗi điểm thành một điểm sao cho khoảng cách từ điểm đó đến tâm quay không đổi và góc giữa hai đoạn thẳng nối điểm ban đầu và điểm ảnh với tâm quay là một góc cố định.
Phép đối xứng trục: Biến đổi mỗi điểm thành một điểm sao cho đường trung trực của đoạn thẳng nối hai điểm tương ứng là một trục cố định.
Phép đối xứng tâm: Biến đổi mỗi điểm thành một điểm sao cho trung điểm của đoạn thẳng nối hai điểm tương ứng là một tâm cố định.

Ví dụ minh họa:

Giả sử bài toán yêu cầu tìm ảnh của điểm A(1; 2) qua phép tịnh tiến theo vectơ v = (3; -1). Để giải bài toán này, ta áp dụng công thức:

A'(x'; y') = A(x; y) + v(a; b) = (x + a; y + b)

Thay số vào, ta có: A'(1 + 3; 2 - 1) = A'(4; 1). Vậy ảnh của điểm A qua phép tịnh tiến là A'(4; 1).

Mẹo giải nhanh và hiệu quả

Vẽ hình: Vẽ hình minh họa giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Sử dụng công thức: Nắm vững các công thức liên quan đến các phép biến hình để áp dụng một cách chính xác.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự và luyện tập thêm

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về phép biến hình, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết hơn.

Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín

tusach.vn tự hào là một trong những nguồn tài liệu học tập Toán 11 uy tín và được tin cậy bởi đông đảo học sinh và giáo viên. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết, và các bài tập luyện tập để giúp các em học tập hiệu quả và đạt kết quả cao trong môn Toán.

Chúc các em học tập tốt!