Giải bài 5 trang 122 Toán 11 Chân trời sáng tạo tập 1

Giải bài 5 trang 122 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 5 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1

Tusach.vn xin giới thiệu lời giải chi tiết bài 5 trang 122 SBT Toán 11 Chân trời sáng tạo tập 1. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo tập 1.

Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 5 trang 122 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).

Lời giải chi tiết

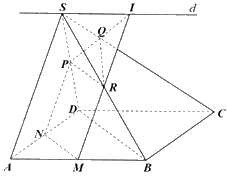
Giải bài 5 trang 122 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

Gọi N, P, R lần lượt là trung điểm của AD, SD, SB.

Vì M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác ABD. Do đó, MN//BD.

Vì P, R lần lượt là trung điểm của SD, SB nên PR là đường trung bình của tam giác SBD. Do đó, PR//BD.

Vì MN//BD, PR//BD nên MN//PR.

Suy ra bốn điểm M, N, P, R tạo thành mặt phẳng (MNPR).

Ta có: MN//BD, \(MN \subset \left( {MNPR} \right)\), BD không nằm trong mặt phẳng (MNPR) nên BD//(MNPR).

Chứng minh tương tự ta có: SA//(MNPR).

Vì mặt phẳng (MNPR) đi qua M và song song với BD, SA nên (MNPR) là mặt phẳng \(\left( \alpha \right)\).

Trong mặt phẳng (SAB), vẽ đường thẳng d đi qua S và d//AB//CD.

Khi đó, giả sử MR cắt d tại I, PI cắt SC tại Q. Suy ra, mặt phẳng \(\left( \alpha \right)\) là (MNPI).

Ta có: \(MN \subset \left( {ABCD} \right),MN \subset \left( {MNPI} \right)\) nên \(\left( {MNPI} \right) \cap \left( {ABCD} \right) = MN\) hay \(\left( \alpha \right) \cap \left( {ABCD} \right) = MN\).

Tương tự ta có:

\(\left( \alpha \right) \cap \left( {SAD} \right) = NP,\left( \alpha \right) \cap \left( {SCD} \right) = PQ,\left( \alpha \right) \cap \left( {SBC} \right) = QR,\left( \alpha \right) \cap \left( {ABS} \right) = MR\)

Giải bài 5 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1: Tổng quan và hướng dẫn chi tiết

Bài 5 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ định nghĩa, tính chất của phép biến hình affine và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình affine.

Nội dung bài tập 5 trang 122 SBT Toán 11 Chân trời sáng tạo tập 1

Bài tập 5 thường bao gồm các dạng câu hỏi sau:

Xác định phép biến hình affine dựa trên các thông tin cho trước.
Tìm ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình affine.
Chứng minh một phép biến hình là phép biến hình affine.
Vận dụng phép biến hình affine để giải quyết các bài toán hình học.

Hướng dẫn giải bài 5 trang 122 SBT Toán 11 Chân trời sáng tạo tập 1

Để giải quyết bài tập này một cách hiệu quả, học sinh cần:

Nắm vững định nghĩa và tính chất của phép biến hình affine.
Hiểu rõ cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình affine.
Sử dụng các công thức và định lý liên quan đến phép biến hình affine.
Rèn luyện kỹ năng giải toán thông qua việc làm nhiều bài tập khác nhau.

Lời giải chi tiết bài 5 trang 122 SBT Toán 11 Chân trời sáng tạo tập 1

Dưới đây là lời giải chi tiết cho bài 5 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1:

Bài 5: (Giả sử đây là nội dung bài tập cụ thể, cần thay thế bằng nội dung thực tế)

Lời giải:

...

Các bài tập tương tự và tài liệu tham khảo

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng có thể tìm kiếm các bài giảng trực tuyến và các video hướng dẫn giải toán trên internet.

Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín

Tusach.vn là một website cung cấp đầy đủ và chính xác các lời giải bài tập Toán 11 Chân trời sáng tạo tập 1. Chúng tôi cam kết mang đến cho học sinh những tài liệu học tập chất lượng cao, giúp các em học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Chương	Bài	Liên kết
1	Bài 1	Giải bài 1 trang 10
1	Bài 2	Giải bài 2 trang 15

Hy vọng với lời giải chi tiết và hướng dẫn giải bài 5 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán Toán 11.