Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 4 trang 112 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho \(EB > AE,AF > FC,BG > GD\). Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Đề bài
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho \(EB > AE,AF > FC,BG > GD\). Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).
Lời giải chi tiết
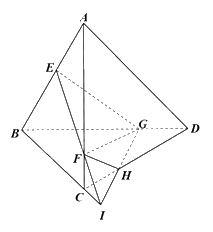
Ta có, EF là giao tuyến của hai mặt phẳng (EFG) và (ABC).
Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD.
Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {ACD} \right),H \in IG \subset \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right),F \in FE \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ACD) là FH.
Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {BCD} \right),H \in IG \subset \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (BCD) là GH.
Vì \(\left\{ \begin{array}{l}E \in AB \subset \left( {ABD} \right),E \in FE \subset \left( {EFG} \right)\\G \in BD \subset \left( {ABD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ABD) là GE.
Giải bài 4 trang 112 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan
Bài 4 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và tính chất của các phép biến hình là vô cùng quan trọng để giải quyết bài toán này một cách hiệu quả.
Nội dung bài tập
Bài 4 thường bao gồm các dạng bài tập sau:
- Xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép biến hình: Học sinh cần xác định được tọa độ của điểm ảnh sau khi thực hiện phép biến hình.
- Tìm phép biến hình biến một hình này thành một hình khác: Yêu cầu học sinh xác định các thông số của phép biến hình (ví dụ: tâm quay, góc quay, vector tịnh tiến, trục đối xứng).
- Chứng minh một tính chất hình học sử dụng phép biến hình: Sử dụng phép biến hình để chứng minh hai hình bằng nhau hoặc hai đường thẳng song song, vuông góc.
Lời giải chi tiết bài 4 trang 112
Để giúp các em hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng phần của bài 4:
Câu a)
(Giả sử đề bài là tìm ảnh của điểm A(1;2) qua phép tịnh tiến theo vector v = (3;-1))
Lời giải:
Gọi A'(x'; y') là ảnh của A qua phép tịnh tiến theo vector v. Khi đó:
- x' = x + vx = 1 + 3 = 4
- y' = y + vy = 2 + (-1) = 1
Vậy A'(4;1).
Câu b)
(Giả sử đề bài là tìm tâm quay và góc quay của phép quay biến điểm A(0;1) thành điểm A'(-1;0))
Lời giải:
Gọi I(x;y) là tâm quay và φ là góc quay. Ta có:
IA = IA' và góc AIA' = φ
Giải hệ phương trình để tìm x, y và φ.
Mẹo giải bài tập phép biến hình
- Nắm vững định nghĩa và tính chất của từng phép biến hình: Đây là nền tảng để giải quyết mọi bài toán.
- Vẽ hình minh họa: Việc vẽ hình sẽ giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng công thức một cách chính xác: Kiểm tra lại các công thức trước khi áp dụng vào bài toán.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp các em làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Tài liệu tham khảo
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
- Các trang web học toán trực tuyến
- Các video hướng dẫn giải bài tập trên YouTube
- Các diễn đàn trao đổi kiến thức toán học
Kết luận
Hy vọng với lời giải chi tiết và những mẹo giải bài tập trên, các em sẽ tự tin hơn khi giải bài 4 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các em học tốt và đạt kết quả cao trong môn Toán!