Giải bài 12 trang 77 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 12 trang 77 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Bài 12 trang 77 SBT Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với các lưu ý quan trọng để bạn có thể tự tin giải quyết bài tập này.
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
Đề bài
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
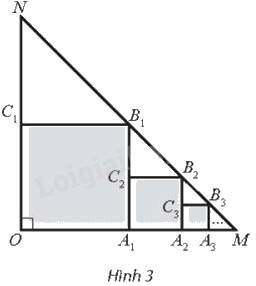
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn để tính tổng: Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn. Cấp số nhân lùi vô hạn này có tổng là: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
Độ dài cạnh của các hình vuông lần lượt là:
\({a_1} = \frac{1}{2},{a_2} = \frac{1}{2}{a_1} = \frac{1}{2}.\frac{1}{2} = {\left( {\frac{1}{2}} \right)^2},{a_3} = \frac{1}{2}{a_2} = \frac{1}{2}{\left( {\frac{1}{2}} \right)^2} = {\left( {\frac{1}{2}} \right)^3},...\)
Diện tích của các hình vuông lần lượt là:
\({S_1} = a_1^2 = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4},\)
\({S_2} = a_2^2 = {\left( {{{\left( {\frac{1}{2}} \right)}^2}} \right)^2} = {\left( {\frac{1}{4}} \right)^2},\)
\({S_3} = a_3^2 = {\left( {{{\left( {\frac{1}{2}} \right)}^3}} \right)^2} = {\left( {\frac{1}{4}} \right)^3},...\)
Các diện tích \({S_1},{S_2},{S_3},...\) lập thành một cấp số nhân lùi vô hạn với số hạng đầu là \({S_1} = \frac{1}{4}\) và công bội bằng \(\frac{1}{4}\).
Do đó, tổng diện tích các hình vuông là: \(S = \frac{1}{4}.\frac{1}{{1 - \frac{1}{4}}} = \frac{1}{3}\)
Giải bài 12 trang 77 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải
Bài 12 trang 77 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất của dãy số để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản sau:
- Dãy số: Định nghĩa, các loại dãy số (dãy số tăng, dãy số giảm, dãy số không đổi).
- Cấp số cộng: Định nghĩa, công thức tính số hạng tổng quát, tổng của n số hạng đầu tiên.
- Cấp số nhân: Định nghĩa, công thức tính số hạng tổng quát, tổng của n số hạng đầu tiên.
Lời giải chi tiết bài 12 trang 77 SBT Toán 11 Chân trời sáng tạo tập 1
Để cung cấp lời giải chính xác, chúng ta cần biết nội dung cụ thể của bài tập 12 trang 77. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận và giải quyết một bài tập tương tự:
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm số hạng thứ 10 của một cấp số cộng có số hạng đầu u1 = 2 và công sai d = 3.
- Xác định các yếu tố đã cho: u1 = 2, d = 3, n = 10.
- Áp dụng công thức tính số hạng tổng quát của cấp số cộng: un = u1 + (n - 1)d
- Thay số vào công thức: u10 = 2 + (10 - 1) * 3 = 2 + 9 * 3 = 2 + 27 = 29
- Kết luận: Số hạng thứ 10 của cấp số cộng là 29.
Các dạng bài tập thường gặp và phương pháp giải
Ngoài việc tìm số hạng tổng quát, bài tập về dãy số, cấp số cộng và cấp số nhân còn có thể yêu cầu:
- Tìm công sai hoặc công bội của cấp số.
- Tính tổng của n số hạng đầu tiên của cấp số.
- Xác định xem một dãy số có phải là cấp số cộng hay cấp số nhân hay không.
- Giải các bài toán ứng dụng thực tế liên quan đến dãy số.
Để giải quyết các dạng bài tập này, bạn cần:
- Nắm vững các công thức và tính chất của dãy số, cấp số cộng và cấp số nhân.
- Đọc kỹ đề bài và xác định đúng các yếu tố đã cho.
- Lựa chọn phương pháp giải phù hợp.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Lưu ý quan trọng khi giải bài tập
Khi giải bài tập về dãy số, cấp số cộng và cấp số nhân, bạn cần lưu ý:
- Đơn vị của các số hạng phải thống nhất.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả bằng cách thay các giá trị đã tìm được vào công thức.
Tổng kết
Bài 12 trang 77 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về dãy số, cấp số cộng và cấp số nhân. Bằng cách nắm vững các công thức và tính chất, cùng với việc luyện tập thường xuyên, bạn sẽ có thể tự tin giải quyết mọi bài tập liên quan đến chủ đề này. tusach.vn hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp bạn học tập hiệu quả hơn.