Giải bài 8 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 8 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 8 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.
Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết bài toán này một cách hiệu quả.
Một chất điểm dao động điều hòa theo phương trình \(s = 3\sin \left( {\frac{\pi }{2}t} \right)\) với s tính bằng cm và t tính bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì \(s \le - \frac{3}{2}\).
Đề bài
Một chất điểm dao động điều hòa theo phương trình \(s = 3\sin \left( {\frac{\pi }{2}t} \right)\) với s tính bằng cm và t tính bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì \(s \le - \frac{3}{2}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đồ thị hàm số \(y = \sin u\left( x \right)\) để giải.
Lời giải chi tiết
Trong 4 giây đầu, ta có \(0 \le t \le 4\), suy ra: \(0 \le \frac{\pi }{2}t \le 2\pi \).
Đặt \(x = \frac{\pi }{2}t\), khi đó \(x \in \left[ {0;2\pi } \right]\). Đồ thị của hàm số \(y = \sin x\) trên đoạn \(\left[ {0;2\pi } \right]\) là:
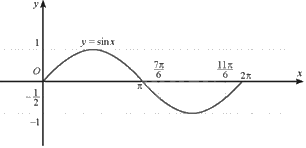
Dựa vào đồ thị trên đoạn \(\left[ {0;2\pi } \right]\), ta có:
\(s \le \frac{{ - 3}}{2}\) khi \(3\sin x \le \frac{{ - 1}}{2}\), suy ra \(\frac{{7\pi }}{6} \le x \le \frac{{11\pi }}{6}\). Do đó, \(\frac{7}{3} \le t \le \frac{{11}}{3}\)
Giải bài 8 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải
Bài 8 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, tính chất của hàm số lượng giác và sử dụng đồ thị để tìm nghiệm hoặc giải các bài toán thực tế.
Nội dung chi tiết bài 8 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1
Để giải quyết bài 8 trang 27 một cách hiệu quả, chúng ta cần phân tích kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập sẽ yêu cầu:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Tìm các điểm cực trị của hàm số.
- Vẽ đồ thị của hàm số.
- Giải các phương trình hoặc bất phương trình liên quan đến hàm số.
Lời giải chi tiết bài 8 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1
Dưới đây là lời giải chi tiết cho bài 8 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng và dễ hiểu:
Ví dụ minh họa (Giả sử bài toán yêu cầu tìm tập xác định của hàm số y = √(2sin(x) - 1))
Để tìm tập xác định của hàm số y = √(2sin(x) - 1), ta cần đảm bảo biểu thức dưới dấu căn lớn hơn hoặc bằng 0:
2sin(x) - 1 ≥ 0
sin(x) ≥ 1/2
Giải bất phương trình lượng giác sin(x) ≥ 1/2, ta được:
π/6 + k2π ≤ x ≤ 5π/6 + k2π, với k ∈ Z
Vậy tập xác định của hàm số là D = [π/6 + k2π; 5π/6 + k2π], với k ∈ Z.
Các dạng bài tập tương tự và phương pháp giải
Ngoài bài 8 trang 27, sách bài tập Toán 11 Chân trời sáng tạo tập 1 còn có nhiều bài tập tương tự. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
- Sử dụng các công thức lượng giác cơ bản.
- Biến đổi biểu thức lượng giác về dạng đơn giản.
- Sử dụng đồ thị hàm số để tìm nghiệm.
- Phân tích bài toán và lựa chọn phương pháp giải phù hợp.
Mẹo giải nhanh bài tập Toán 11 Chân trời sáng tạo tập 1
Để giải nhanh các bài tập Toán 11 Chân trời sáng tạo tập 1, bạn nên:
- Nắm vững kiến thức cơ bản về hàm số lượng giác.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng.
- Kiểm tra lại kết quả sau khi giải xong.
Tài liệu tham khảo hữu ích
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 Chân trời sáng tạo.
- Sách bài tập Toán 11 Chân trời sáng tạo.
- Các trang web học Toán trực tuyến uy tín.
- Các video bài giảng Toán 11 trên YouTube.
Kết luận
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết bài 8 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 một cách hiệu quả. Chúc bạn học tập tốt!