Đề bài
Một cửa hàng sách thống kê số truyện thiếu nhi bán được trong hai tháng ở bảng sau:
Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
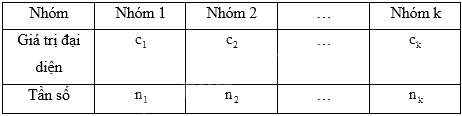
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết
Ta hiệu chỉnh được bảng tần số ghép nhóm gồm các giá trị đại diện của nhóm là:
Cỡ mẫu \(n = 61\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{17.5 + 24.7 + 31.25 + 38.15 + 45.9}}{{61}} = \frac{{2\;003}}{{61}}\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {27,5;34,5} \right)\).
Do đó, \({u_m} = 27,5,{u_{m + 1}} = 34,5,{n_m} = 25,{n_{m + 1}} = 15,{u_{m + 1}} - {u_m} = 34,5 - 27,5 = 7\)
Mốt của mẫu số liệu là: \({M_O} = 27,5 + \frac{{25 - 7}}{{\left( {25 - 7} \right) + \left( {25 - 15} \right)}}.7 = 32\)
Gọi \({x_1},{x_2},...,{x_{61}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_5} \in \left[ {13,5;20,5} \right),{x_6},...,{x_{12}} \in \left[ {20,5;27,5} \right),{x_{13}},...,{x_{37}} \in \left[ {27,5;34,5} \right),\) \({x_{38}},...,{x_{52}} \in \left[ {34,5;41,5} \right),{x_{53}},...,{x_{61}} \in \left[ {41,5;48,5} \right)\).
Do cỡ mẫu \(n = 61\) nên tứ phân vị thứ hai của mẫu số liệu là \({x_{31}}\). Do đó tứ phân vị thứ hai của mẫu số liệu thuộc nhóm \(\left[ {27,5;34,5} \right)\).
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:
\({Q_2} = 27,5 + \frac{{\frac{{61}}{2} - \left( {5 + 7} \right)}}{{25}}.\left( {34,5 - 27,5} \right) = \frac{{817}}{{25}}\)
Do cỡ mẫu \(n = 61\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {27,5;34,5} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 27,5 + \frac{{\frac{{61}}{4} - \left( {5 + 7} \right)}}{{25}}.\left( {34,5 - 27,5} \right) = 28,41\)
Do cỡ mẫu \(n = 61\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{46}} + {x_{47}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {34,5;41,5} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 34,5 + \frac{{\frac{{3.61}}{4} - \left( {5 + 7 + 25} \right)}}{{15}}.\left( {41,5 - 34,5} \right) = \frac{{463}}{{12}}\)
