Giải bài 2 trang 121 Toán 11 - Chân trời sáng tạo tập 1

Giải bài 2 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 2 trang 121 sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Tusach.vn xin giới thiệu lời giải chi tiết bài 2 trang 121 SBT Toán 11 Chân trời sáng tạo tập 1. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’. a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE). b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho \(AM = \frac{1}{3}AF,\) \(AN = \frac{1}{3}AD\). Chứng minh MN//(DCEF).

Đề bài

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.

a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).

b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho \(AM = \frac{1}{3}AF,\) \(AN = \frac{1}{3}AD\). Chứng minh MN//(DCEF).

Phương pháp giải - Xem chi tiết Giải bài 2 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).

Lời giải chi tiết

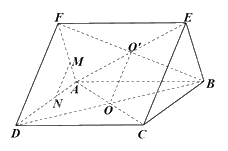
Giải bài 2 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

a) Vì O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.

Vì O là trung điểm của BD, O’ là trung điểm của BF nên OO’ là đường trung bình của tam giác BDF. Do đó, OO’//DF (1)

Vì O là trung điểm của AC, O’ là trung điểm của AE nên OO’ là đường trung bình của tam giác ACE. Do đó, OO’//CE (2)

Từ (1) và (2) ta có: OO’//DF//CE

Vì OO’//DF, OO’ không nằm trên mặt phẳng (ADF) và \(DF \subset \left( {ADF} \right)\) nên OO’//(ADF).

Vì OO’//CE, OO’ không nằm trên mặt phẳng (BCE) và \(CE \subset \left( {BCE} \right)\) nên OO’//(BCE).

b) Vì \(AM = \frac{1}{3}AF,AN = \frac{1}{3}AD \Rightarrow \frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\)

Tam giác ADF có: \(\frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\) nên MN//DF (định lí Thalès đảo)

Vì MN//DF, MN không nằm trên mặt phẳng (DCEF) và \(DF \subset \left( {DCEF} \right)\) nên MN//(DCEF).

Giải bài 2 trang 121 sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan và hướng dẫn chi tiết

Bài 2 trang 121 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học kỳ 1, tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa, tính chất của phép biến hình affine và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình affine.

Nội dung bài tập

Bài 2 thường bao gồm các dạng bài tập sau:

Xác định phép biến hình affine dựa trên các thông tin cho trước (ví dụ: ảnh của một số điểm).
Tìm ảnh của một điểm, một đường thẳng, một đường tròn qua một phép biến hình affine cho trước.
Chứng minh một phép biến hình là phép biến hình affine.
Vận dụng phép biến hình affine để giải quyết các bài toán hình học.

Lời giải chi tiết bài 2 trang 121

Để giải bài 2 trang 121 sách bài tập Toán 11 Chân trời sáng tạo tập 1, bạn cần thực hiện các bước sau:

Bước 1: Đọc kỹ đề bài và xác định yêu cầu của bài toán.
Bước 2: Xác định các thông tin đã cho (ví dụ: tọa độ các điểm, phương trình đường thẳng, ma trận của phép biến hình affine).
Bước 3: Áp dụng định nghĩa, tính chất của phép biến hình affine để giải quyết bài toán.
Bước 4: Kiểm tra lại kết quả và đảm bảo rằng đáp án của bạn là chính xác.

Ví dụ minh họa:

Giả sử cho phép biến hình affine f xác định bởi:

f(x; y) = (x + 2y; 3x - y)

Tìm ảnh của điểm A(1; 2) qua phép biến hình f.

Lời giải:

Áp dụng công thức của phép biến hình f, ta có:

f(1; 2) = (1 + 2*2; 3*1 - 2) = (5; 1)

Vậy ảnh của điểm A(1; 2) qua phép biến hình f là điểm A'(5; 1).

Mẹo giải bài tập

Nắm vững định nghĩa và tính chất của phép biến hình affine.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ (ví dụ: máy tính cầm tay, phần mềm hình học) để kiểm tra kết quả.
Tham khảo các lời giải chi tiết trên tusach.vn để hiểu rõ hơn về cách giải bài tập.

Tài liệu tham khảo

Ngoài sách bài tập Toán 11 Chân trời sáng tạo tập 1, bạn có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 11 Chân trời sáng tạo tập 1.
Các bài giảng trực tuyến về phép biến hình affine.
Các trang web, diễn đàn học tập trực tuyến.

Kết luận

Bài 2 trang 121 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình affine. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các bạn học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các bạn học tốt!