Giải bài 3 trang 8 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Tổng quan nội dung
Giải bài 3 trang 8 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 8 Sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu và lời giải chính xác, dễ hiểu.
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
Đề bài
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
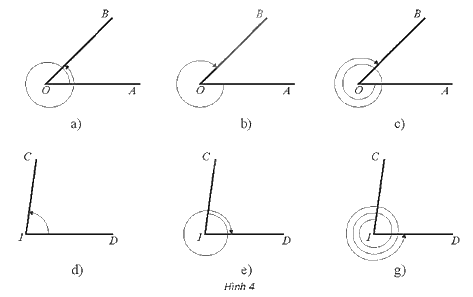
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khái niệm góc lượng giác:
a, b, c) Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác nhau một bội nguyên của \({360^0}\) nên có công thức tổng quát là: \(\left( {Oa,Ob} \right) = {\alpha ^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)\) với \({\alpha ^0}\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
d, e, g) Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai nhau khác một bội nguyên của \(2\pi \) nên ta có công thức tổng quát là \(\left( {Oa,Ob} \right) = \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\) với \(\alpha \) là số đo theo radian của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Lời giải chi tiết
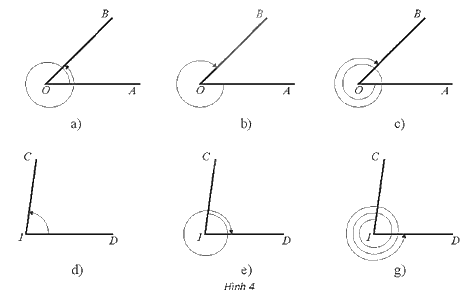
Số đo của góc lượng giác (OA, OB) trong Hình 4a là: \(\frac{\pi }{4} + 2\pi = \frac{{9\pi }}{4}\)
Số đo của góc lượng giác (OA, OB) trong Hình 4b là: \(\frac{\pi }{4} - 2\pi = - \frac{{7\pi }}{4}\)
Số đo của góc lượng giác (OA, OB) trong Hình 4c là: \(\frac{\pi }{4} - 2.2\pi = \frac{{ - 15\pi }}{4}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4d là: \({82^0}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4e là: \( - \left( {{{82}^0} + {{360}^0}} \right) = - {442^0}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4g là: \({360^0} - {82^0} + {2.360^0} = {998^0}\)
Giải bài 3 trang 8 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan
Bài 3 trang 8 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về Hàm số bậc hai. Bài tập này tập trung vào việc xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm tập xác định, tập giá trị, và vẽ đồ thị hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung bài 3 trang 8 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Bài 3 bao gồm các câu hỏi và bài tập sau:
- Xác định hệ số a, b, c của hàm số bậc hai.
- Tìm tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Xác định đỉnh của parabol.
- Vẽ đồ thị hàm số.
Lời giải chi tiết bài 3 trang 8 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Câu a)
Hàm số: y = 2x2 - 5x + 3
- Hệ số a = 2, b = -5, c = 3
- Tập xác định: D = ℝ
- Tập giá trị: y ≥ -7/8 (do a > 0)
- Đỉnh của parabol: I(5/4, -7/8)
Câu b)
Hàm số: y = -x2 + 4x - 1
- Hệ số a = -1, b = 4, c = -1
- Tập xác định: D = ℝ
- Tập giá trị: y ≤ 3 (do a < 0)
- Đỉnh của parabol: I(2, 3)
Phương pháp giải bài tập về hàm số bậc hai
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Công thức tính đỉnh của parabol: I(-b/2a, (4ac - b2)/4a)
- Điều kiện để hàm số bậc hai có tập giá trị là:
- Nếu a > 0: y ≥ (4ac - b2)/4a
- Nếu a < 0: y ≤ (4ac - b2)/4a
- Cách vẽ đồ thị hàm số bậc hai:
- Xác định đỉnh của parabol.
- Xác định các điểm đặc biệt (giao điểm với trục hoành, trục tung).
- Vẽ parabol đi qua các điểm đã xác định.
Lưu ý khi giải bài tập
Khi giải bài tập về hàm số bậc hai, các em cần chú ý:
- Kiểm tra kỹ các hệ số a, b, c.
- Sử dụng đúng công thức tính toán.
- Vẽ đồ thị hàm số một cách chính xác.
Bài tập tương tự
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Kết luận
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh đã hiểu rõ hơn về bài 3 trang 8 Sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các em học tập tốt!