Giải bài 4 trang 27 SBT Toán 11 - Chân trời sáng tạo tập 1

Giải bài 4 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1

Bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất đã học để giải quyết các bài toán thực tế.

tusach.vn xin giới thiệu đáp án chi tiết và cách giải bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh hiểu rõ hơn về bài học và tự tin hơn trong quá trình làm bài tập.

Cho hàm số \(y = \sin x\) với \(x \in \left[ { - 2\pi ;2\pi } \right]\). a) Vẽ đồ thị hàm số đã cho. b) Tìm các giá trị của \(x \in \left[ {\frac{{ - 5\pi }}{3};\frac{{7\pi }}{3}} \right]\) sao cho \(\sin \left( {\frac{\pi }{3} - x} \right) = - 1\).

Đề bài

Cho hàm số \(y = \sin x\) với \(x \in \left[ { - 2\pi ;2\pi } \right]\).

a) Vẽ đồ thị hàm số đã cho.

b) Tìm các giá trị của \(x \in \left[ {\frac{{ - 5\pi }}{3};\frac{{7\pi }}{3}} \right]\) sao cho \(\sin \left( {\frac{\pi }{3} - x} \right) = - 1\).

c) Tìm các giá trị của \(x \in \left[ {\frac{{ - 9\pi }}{8};\frac{{7\pi }}{8}} \right]\) sao cho \(\sin \left( {2x + \frac{\pi }{4}} \right) > 0\).

d) Tìm m để có bốn giá trị \(\alpha \in \left[ { - 2\pi ;2\pi } \right]\) phân biệt thỏa mãn \(\sin \alpha = m\).

Phương pháp giải - Xem chi tiết Giải bài 4 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về đồ thị hàm số \(y = \sin x\) để giải.

Lời giải chi tiết

a) Ta có đồ thị hàm số \(y = \sin x\) với \(x \in \left[ { - 2\pi ;2\pi } \right]\):

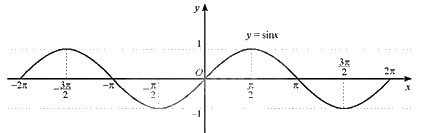
Giải bài 4 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

b) Đặt \(\frac{\pi }{3} - x = t\). Vì \(\frac{{ - 5\pi }}{3} \le x \le \frac{{7\pi }}{3} \Rightarrow - 2\pi \le t \le 2\pi \).

Từ đồ thị hàm số trong phần a, ta có: \(\sin t = - 1\) khi và chỉ khi \(t = \frac{{ - \pi }}{2}\) hoặc \(t = \frac{{3\pi }}{2}\)

Do đó, \(\frac{\pi }{3} - x = \frac{{ - \pi }}{2}\) hoặc \(\frac{\pi }{3} - x = \frac{{3\pi }}{2}\). Suy ra: \(x = \frac{{5\pi }}{6}\) hoặc \(x = \frac{{ - 7\pi }}{6}\)

c) Đặt \(2x + \frac{\pi }{4} = t\). Vì \(\frac{{ - 9\pi }}{8} \le x \le \frac{{7\pi }}{8} \Rightarrow - 2\pi \le t \le 2\pi \).

Từ đồ thị hàm số trong phần a, ta có: \(\sin t > 0\) khi và chỉ khi \( - 2\pi < t < - \pi \) hoặc \(0 < t < \pi \)

Suy ra: \( - 2\pi < 2x + \frac{\pi }{4} < - \pi \) hoặc \(0 < 2x + \frac{\pi }{4} < \pi \)

Do đó, \(\frac{{ - 9\pi }}{8} \le x \le \frac{{ - 5\pi }}{8}\) hoặc \(\frac{{ - \pi }}{8} \le x \le \frac{{3\pi }}{8}\)

d) Có bốn giá trị \(\alpha \in \left[ { - 2\pi ;2\pi } \right]\) phân biệt thỏa mãn \(\sin \alpha = m\) khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \sin \alpha \) tại bốn điểm. Từ đồ thị hàm số ở trên, điều này xảy ra khi và chỉ khi \( - 1 < m < 0\) hoặc \(0 < m < 1\).

Giải bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1: Tổng quan và hướng dẫn giải chi tiết

Bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh áp dụng các công thức tính tổng của cấp số cộng và cấp số nhân, cũng như các tính chất của dãy số để tìm ra kết quả chính xác.

Nội dung bài tập 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1

Thông thường, bài tập 4 sẽ đưa ra một tình huống thực tế liên quan đến dãy số, cấp số cộng hoặc cấp số nhân. Ví dụ, bài tập có thể yêu cầu tính tổng số tiền tiết kiệm sau một số năm nhất định, hoặc tính số lượng sản phẩm được sản xuất trong một khoảng thời gian nhất định.

Phương pháp giải bài tập 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1

Để giải bài tập này một cách hiệu quả, học sinh cần:

Xác định đúng loại dãy số (cấp số cộng, cấp số nhân hoặc dãy số khác).
Tìm ra các yếu tố cần thiết của dãy số (số hạng đầu, công sai/công bội).
Áp dụng công thức tính tổng của cấp số cộng hoặc cấp số nhân (nếu có).
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Đáp án chi tiết bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1

Dưới đây là đáp án chi tiết cho bài 4 trang 27 SBT Toán 11 Chân trời sáng tạo tập 1. (Lưu ý: Đáp án cụ thể sẽ phụ thuộc vào đề bài chính thức. Chúng tôi sẽ cung cấp đáp án khi có đề bài đầy đủ.)

Ví dụ minh họa (giả định đề bài):

Một người gửi tiết kiệm 10 triệu đồng với lãi suất 6%/năm. Sau mỗi năm, tiền lãi được nhập vào vốn gốc. Hỏi sau 5 năm, người đó có bao nhiêu tiền?

Giải:

Đây là một cấp số nhân với:

Số hạng đầu: u₁ = 10 triệu đồng
Công bội: q = 1 + 6% = 1.06
Số số hạng: n = 5

Tổng số tiền sau 5 năm là:

S₅ = u₁ * (q⁵ - 1) / (q - 1) = 10 * (1.06⁵ - 1) / (1.06 - 1) ≈ 13.382.256 đồng

Lưu ý khi giải bài tập về dãy số, cấp số cộng và cấp số nhân

Nắm vững các công thức tính số hạng tổng quát và tổng của cấp số cộng, cấp số nhân.
Chú ý đến điều kiện xác định của các công thức.
Rèn luyện kỹ năng giải các bài toán thực tế để áp dụng kiến thức vào cuộc sống.

Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín

tusach.vn là một trang web cung cấp đầy đủ và chính xác các tài liệu học tập Toán 11, bao gồm:

Giải bài tập sách giáo khoa
Giải bài tập sách bài tập
Các bài giảng video
Các đề thi thử

Hãy truy cập tusach.vn để có thêm nhiều tài liệu học tập hữu ích và đạt kết quả tốt nhất trong môn Toán 11!

Bảng tổng hợp công thức quan trọng

Công thức	Mô tả
u_n = u₁ + (n-1)d	Số hạng tổng quát của cấp số cộng
S_n = n/2 * (u₁ + u_n)	Tổng n số hạng đầu của cấp số cộng
u_n = u₁ * q^n-1	Số hạng tổng quát của cấp số nhân
S_n = u₁ * (qⁿ - 1) / (q - 1)	Tổng n số hạng đầu của cấp số nhân (q ≠ 1)