Giải bài 11 trang 91 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 11 trang 91 SBT Toán 11 Chân trời sáng tạo tập 1. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ lời giải các bài tập trong sách bài tập Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh ôn tập và làm bài tập hiệu quả.
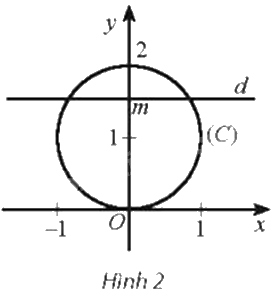
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?
Giải bài 11 trang 91 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan
Bài 11 trang 91 Sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ về các tính chất của phép biến hình affine, cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình affine, và ứng dụng chúng vào việc giải các bài toán hình học.
Nội dung chi tiết bài 11 trang 91
Bài 11 thường bao gồm các dạng bài tập sau:
- Dạng 1: Xác định phép biến hình affine dựa trên các thông tin cho trước (ví dụ: ảnh của ba điểm không thẳng hàng).
- Dạng 2: Tìm ảnh của một điểm, một đường thẳng, một đường tròn qua phép biến hình affine đã cho.
- Dạng 3: Chứng minh một tập hợp các điểm là ảnh của một tập hợp khác qua một phép biến hình affine.
- Dạng 4: Ứng dụng phép biến hình affine để giải các bài toán hình học cụ thể.
Lời giải chi tiết bài 11 trang 91 (Ví dụ)
Bài 11: Trong mặt phẳng, cho hai điểm A(1; 2) và B(3; 4). Tìm phép biến hình affine f biến A thành A'(-1; 0) và B thành B'(5; 2).
Lời giải:
- Bước 1: Tìm vector AB = (3-1; 4-2) = (2; 2).
- Bước 2: Tìm vector A'B' = (5-(-1); 2-0) = (6; 2).
- Bước 3: Tìm ma trận biến đổi M sao cho M.AB = A'B'.
- Bước 4: Giải hệ phương trình để tìm các phần tử của ma trận M.
- Bước 5: Tìm vector t sao cho f(A) = MA + t = A'.
- Bước 6: Viết phương trình của phép biến hình affine f.
Mẹo giải bài tập phép biến hình affine
- Nắm vững định nghĩa và các tính chất của phép biến hình affine.
- Luyện tập các bài tập xác định phép biến hình affine dựa trên các thông tin cho trước.
- Sử dụng các công thức và phương pháp giải bài tập một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải bài tập.
Tài liệu tham khảo hữu ích
Để hiểu rõ hơn về phép biến hình affine và các ứng dụng của nó, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 - Chân trời sáng tạo tập 1
- Sách bài tập Toán 11 - Chân trời sáng tạo tập 1
- Các trang web học Toán trực tuyến uy tín
Kết luận
Bài 11 trang 91 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình affine. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải bài tập này.
