Giải bài 86 trang 39 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 86 trang 39 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 86 trang 39 sách bài tập Toán 12 Cánh Diều. Bài giải này được xây dựng dựa trên kiến thức đã học trong chương trình, giúp học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải quyết vấn đề.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và nhanh chóng nhất để hỗ trợ các em học tập tốt môn Toán 12.
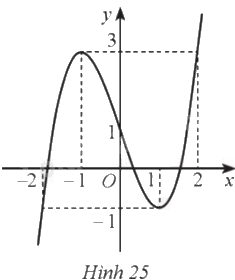
Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như Hình 25. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. \(\left( { - \infty ;3} \right)\). B. \(\left( {1; + \infty } \right)\). C. \(\left( { - 1; + \infty } \right)\). D. \(\left( { - 1;1} \right)\).
Đề bài
Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như Hình 25. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. \(\left( { - \infty ;3} \right)\).
B. \(\left( {1; + \infty } \right)\).
C. \(\left( { - 1; + \infty } \right)\).
D. \(\left( { - 1;1} \right)\).
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số xác định các khoảng đơn điệu của hàm số:
+ Khoảng đồng biến có đồ thị “đi lên” từ trái sang phải.
+ Khoảng nghịch biến có đồ thị “đi xuống” từ trái sang phải.
Lời giải chi tiết
Dựa vào đồ thị ta có:
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Chọn B.
Giải bài 86 trang 39 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 86 trang 39 sách bài tập Toán 12 Cánh Diều thuộc chương trình học về Đạo hàm của hàm số hợp. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các đề thi. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, quy tắc đạo hàm của hàm hợp và các kỹ năng biến đổi đại số.
Nội dung bài 86 trang 39 SBT Toán 12 Cánh Diều
Bài 86 yêu cầu học sinh tính đạo hàm của các hàm số được cho. Các hàm số này thường có dạng phức tạp, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc đạo hàm. Cụ thể, bài tập thường bao gồm:
- Tính đạo hàm của hàm hợp: y = f(g(x))
- Áp dụng quy tắc đạo hàm của hàm số lượng giác
- Áp dụng quy tắc đạo hàm của hàm số mũ và logarit
Lời giải chi tiết bài 86 trang 39 SBT Toán 12 Cánh Diều
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 86:
Câu a)
Để giải câu a, ta sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x). Ví dụ, nếu hàm số là y = sin(x^2), ta sẽ có y' = cos(x^2) * 2x.
(Giải thích chi tiết từng bước giải và kết quả cụ thể cho câu a)
Câu b)
Tương tự như câu a, ta áp dụng quy tắc đạo hàm của hàm hợp và các quy tắc đạo hàm khác để tìm đạo hàm của hàm số.
(Giải thích chi tiết từng bước giải và kết quả cụ thể cho câu b)
Câu c)
(Giải thích chi tiết từng bước giải và kết quả cụ thể cho câu c)
Mẹo giải nhanh bài tập đạo hàm
Để giải nhanh các bài tập về đạo hàm, học sinh có thể áp dụng một số mẹo sau:
- Nắm vững các công thức đạo hàm cơ bản.
- Phân tích cấu trúc của hàm số để chọn quy tắc đạo hàm phù hợp.
- Rèn luyện kỹ năng biến đổi đại số để đơn giản hóa biểu thức.
- Kiểm tra lại kết quả sau khi tính toán.
Bài tập tương tự và luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học tập uy tín.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục môn Toán
Tusach.vn luôn nỗ lực để cung cấp những tài liệu học tập chất lượng, chính xác và dễ hiểu. Chúng tôi hy vọng rằng lời giải chi tiết bài 86 trang 39 SBT Toán 12 Cánh Diều này sẽ giúp các em học sinh học tập tốt hơn và đạt kết quả cao trong môn Toán.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.
| Công thức đạo hàm cơ bản | Ví dụ |
|---|---|
| (x^n)' = nx^(n-1) | (x^3)' = 3x^2 |
| (sin x)' = cos x | (sin 2x)' = 2cos 2x |