Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) \(y = \left( {x - 2} \right){\left( {x + 1} \right)^2}\);
b) \(y = - \frac{1}{3}{x^3} - {x^2} + 2\);
c) \(y = 2{{\rm{x}}^3} - 3{{\rm{x}}^2} + 2{\rm{x}} - 1\);
d) \(y = - \frac{1}{4}\left( {{x^3} - 6{{\rm{x}}^2} + 12{\rm{x}}} \right)\).
Phương pháp giải - Xem chi tiết
Sơ đồ khảo sát hàm số:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
• Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm các đường tiệm cận của đồ thị (nếu có).
• Lập bảng biến thiên của hàm số, bao gồm: tính đạo hàm của hàm số, xét dấu đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng.
Bước 3. Vẽ đồ thị hàm số
• Vẽ các đường tiệm cận (nếu có).
• Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục toạ độ (trong trường hợp đơn giản),…
• Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
Lời giải chi tiết
a) \(y = \left( {x - 2} \right){\left( {x + 1} \right)^2} = {x^3} - 3{\rm{x}} - 2\)
1) Tập xác định: \(\mathbb{R}\).
2) Sự biến thiên:
• Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
• Bảng biến thiên:
\(y' = 3{{\rm{x}}^2} - 3\) và \(y' = 0 \Leftrightarrow x = - 1\) hoặc \({\rm{x}} = 1\).
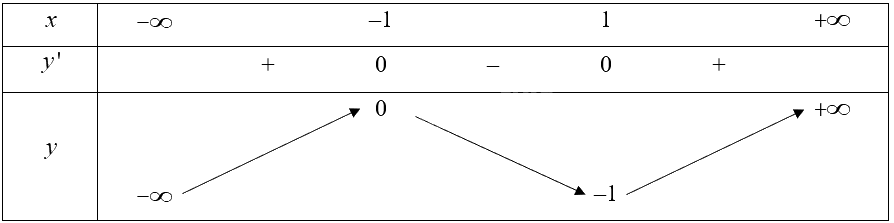
Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\); đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đạt cực tiểu tại \(x = 1,{y_{CT}} = - 4\); hàm số đạt cực đại tại \(x = -1,{y_{CĐ}} = 0\).
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(\left( {0; - 2} \right)\).
• Đồ thị hàm số đi qua các điểm: \(\left( { - 2; - 4} \right),\left( { - 1;0} \right),\left( {0; - 2} \right),\left( {1; - 4} \right),\left( {2;0} \right)\).
Vậy đồ thị hàm số \(y = \left( {x - 2} \right){\left( {x + 1} \right)^2}\) như sau:
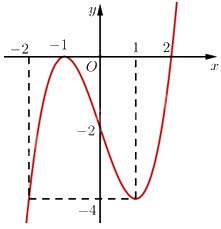
Tâm đối xứng của đồ thị hàm số đó là điểm \(I\left( {0; - 2} \right)\).
b) 1) Tập xác định: \(\mathbb{R}\).
2) Sự biến thiên:
• Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \).
• Bảng biến thiên:
\(y' = - {{\rm{x}}^2} - 2{\rm{x}}\) và \(y' = 0 \Leftrightarrow x = - 2\) hoặc \({\rm{x}} = 0\).
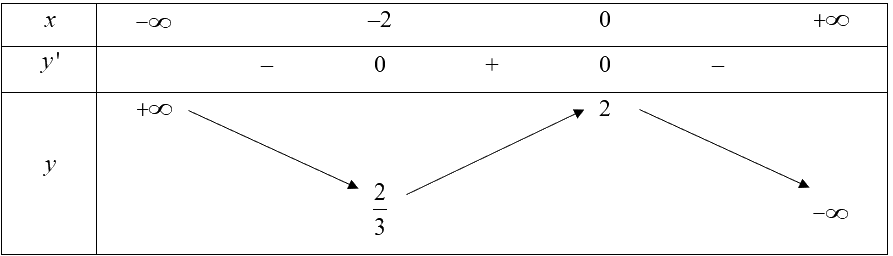
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\); đồng biến trên khoảng \(\left( { - 2;0} \right)\).
Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = \frac{2}{3}\); hàm số đạt cực đại tại \(x = 0,{y_{CĐ}} = 2\).
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(\left( {0;2} \right)\).
• Đồ thị hàm số đi qua các điểm: \(\left( { - 3;2} \right),\left( { - 2;\frac{2}{3}} \right),\left( { - 1;\frac{4}{3}} \right),\left( {0;2} \right),\left( {1;\frac{2}{3}} \right)\).
Vậy đồ thị hàm số \(y = - \frac{1}{3}{x^3} - {x^2} + 2\) như sau:
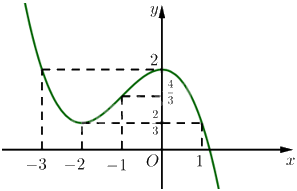
Tâm đối xứng của đồ thị hàm số đó là điểm \(I\left( { - 1;\frac{4}{3}} \right)\).
c) 1) Tập xác định: \(\mathbb{R}\).
2) Sự biến thiên:
• Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
• Bảng biến thiên:
\(y' = 6{{\rm{x}}^2} - 6{\rm{x}} + 2 = 6{\left( {x - \frac{1}{2}} \right)^2} + \frac{1}{2} > 0,\forall x \in \mathbb{R}\).
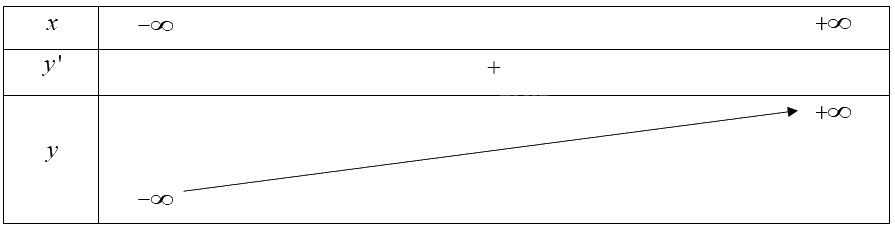
Hàm số đồng biến trên \(\mathbb{R}\).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(\left( {0; - 1} \right)\).
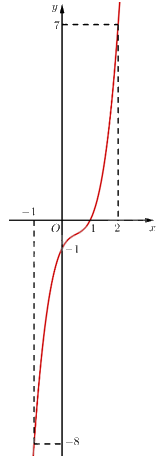
• Đồ thị hàm số đi qua các điểm: \(\left( { - 1; - 8} \right),\left( {0; - 1} \right),\left( {1;0} \right),\left( {2;7} \right)\).
Vậy đồ thị hàm số \(y = 2{{\rm{x}}^3} - 3{{\rm{x}}^2} + 2{\rm{x}} - 1\) như hình bên:
Tâm đối xứng của đồ thị hàm số đó là điểm \(I\left( {\frac{1}{2}; - \frac{1}{2}} \right)\).
d) \(y = - \frac{1}{4}\left( {{x^3} - 6{{\rm{x}}^2} + 12{\rm{x}}} \right) = - \frac{1}{4}{x^3} + \frac{3}{2}{{\rm{x}}^2} - 3{\rm{x}}\)
1) Tập xác định: \(\mathbb{R}\).
2) Sự biến thiên:
• Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \).
• Bảng biến thiên:
\(y' = - \frac{3}{4}{{\rm{x}}^2} + 3{\rm{x}} - 3\) và \(y' = 0 \Leftrightarrow x = 2\).
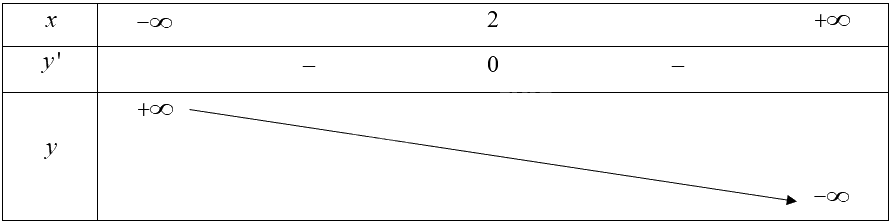
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số không có cực trị.
3) Đồ thị
• Giao điểm của đồ thị với trục tung: \(O\left( {0;0} \right)\).
• Đồ thị hàm số đi qua các điểm: \(\left( {0;0} \right),\left( {1; - \frac{7}{4}} \right),\left( {2; - 2} \right),\left( {3; - \frac{9}{4}} \right),\left( {4; - 4} \right)\).
Vậy đồ thị hàm số \(y = - \frac{1}{3}{x^3} - {x^2} + 2\) như sau:
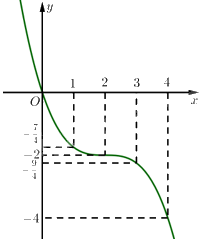
Tâm đối xứng của đồ thị hàm số đó là điểm \(I\left( {2; - 2} \right)\).
