Giải bài 16 trang 95 sách bài tập toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 16 trang 95 SBT Toán 12 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 16 trang 95 sách bài tập Toán 12 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách bài tập Toán 12 Cánh Diều.
Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.
Đề bài
Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.
Phương pháp giải - Xem chi tiết
‒ Sử dụng sơ đồ hình cây.
‒ Sử dụng công thức tính xác suất toàn phần: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết
Xét các biến cố:
\(A\): “Chọn được xạ thủ hạng I”;
\(B\): “Viên đạn đó trúng mục tiêu”;
Có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II nên ta có
\(P\left( A \right) = \frac{4}{{10}} = 0,4;P\left( {\overline A } \right) = \frac{6}{{10}} = 0,6\)
Xác suất bắn trúng mục tiêu của xạ thủ hạng I và 0,75 nên ta có \(P\left( {B|A} \right) = 0,75\).
Xác suất bắn trúng mục tiêu của xạ thủ hạng II và 0,6 nên ta có \(P\left( {B|\overline A } \right) = 0,6\).
Ta có sơ đồ hình cây như sau: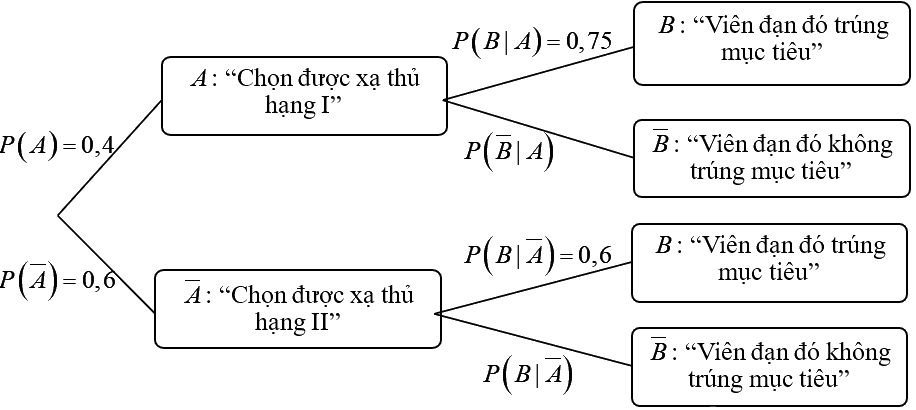
Vậy xác suất của biến cố \(B\): “Viên đạn đó trúng mục tiêu” là:
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = 0,4.0,75 + 0,6.0,6 = 0,66\).
Giải bài 16 trang 95 SBT Toán 12 Cánh Diều: Tổng quan và Phương pháp giải
Bài 16 trang 95 sách bài tập Toán 12 Cánh Diều thuộc chương trình học Toán 12, tập trung vào chủ đề về Đường thẳng và Mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về:
- Vecto chỉ phương và Vecto pháp tuyến của đường thẳng và mặt phẳng.
- Phương trình đường thẳng và mặt phẳng.
- Quan hệ giữa đường thẳng và mặt phẳng (song song, vuông góc, cắt nhau).
- Tính khoảng cách từ một điểm đến mặt phẳng.
Nội dung chi tiết bài 16 trang 95 SBT Toán 12 Cánh Diều
Bài 16 thường bao gồm các dạng bài tập sau:
- Xác định phương trình đường thẳng đi qua một điểm và song song/vuông góc với một đường thẳng cho trước.
- Xác định phương trình mặt phẳng đi qua một điểm và song song/vuông góc với một mặt phẳng cho trước.
- Tìm giao điểm của đường thẳng và mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ một điểm đến mặt phẳng.
Lời giải chi tiết bài 16 trang 95 SBT Toán 12 Cánh Diều
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 16 trang 95 SBT Toán 12 Cánh Diều:
Câu 1: (Ví dụ minh họa)
Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z = 5. Tìm tọa độ giao điểm của d và (P).
Lời giải:
Thay phương trình tham số của d vào phương trình (P), ta được:
2(1 + t) - (2 - t) + (3 + 2t) = 5
2 + 2t - 2 + t + 3 + 2t = 5
5t + 3 = 5
5t = 2
t = 2/5
Thay t = 2/5 vào phương trình tham số của d, ta được:
x = 1 + 2/5 = 7/5
y = 2 - 2/5 = 8/5
z = 3 + 2(2/5) = 3 + 4/5 = 19/5
Vậy giao điểm của d và (P) là (7/5, 8/5, 19/5).
Câu 2: (Ví dụ minh họa)
Cho hai điểm A(1; 2; 3) và B(3; 4; 5). Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
Lời giải:
Trung điểm I của AB là I((1+3)/2; (2+4)/2; (3+5)/2) = I(2; 3; 4).
Vecto AB = (3-1; 4-2; 5-3) = (2; 2; 2).
Vecto pháp tuyến của mặt phẳng trung trực là n = AB = (2; 2; 2). Ta có thể chọn n' = (1; 1; 1).
Phương trình mặt phẳng trung trực của AB là:
1(x - 2) + 1(y - 3) + 1(z - 4) = 0
x + y + z - 9 = 0
Mẹo giải nhanh và lưu ý quan trọng
- Nắm vững các công thức về vecto chỉ phương, vecto pháp tuyến, phương trình đường thẳng và mặt phẳng.
- Sử dụng các tính chất đối xứng và quan hệ giữa đường thẳng và mặt phẳng để đơn giản hóa bài toán.
- Kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.
Tusach.vn - Đồng hành cùng bạn học Toán 12
Tusach.vn luôn cố gắng cung cấp những lời giải chi tiết, dễ hiểu và chính xác nhất cho các bài tập Toán 12. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập!